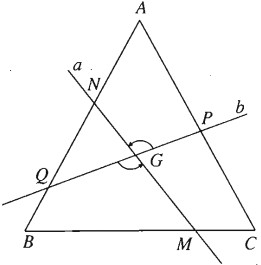
Qua tâm G của tam giác đều ABC, kẻ đường thẳng a cắt BC tại M và cắt AB tại N, kẻ đường thẳng b cắt AC tại P và AB tại Q, đồng thời góc giữa a và b bằng 60°. Chứng minh rằng tứ giác MNPQ là một hình thang cân.

Gọi \({Q_{\left( {G;{{120}^0}} \right)}}\) là phép quay tâm G góc \(120^0\). Phép quay này biến b thành a, biến CA thành AB; do đó nó biến P thành N.
Advertisements (Quảng cáo)
Tương tự \({Q_{\left( {G;{{120}^0}} \right)}}\) cũng biến Q thành M. Từ đó suy ra \(GP = GN,GQ = GM\). Do đó hai tam giác GNQ và GPM bằng nhau, suy ra NQ = PM. Vì \({Q_{\left( {G;{{120}^0}} \right)}}\) biến PQ thành NM nên \(PQ = NM\). Từ đó suy ra hai tam giác \(NQM\) và \(PMQ\) bằng nhau. Do đó \(\widehat {NQM} = \widehat {PMQ}\). Tương tự \(\widehat {QNP} = \widehat {MPN}\).
Từ đó suy ra \(\widehat {PNQ} + \widehat {NQM} = {180^0}\)
Do đó \(NP\parallel QM\). Vậy ta có tứ giác \(MPNQ\) là hình thang cân.
