Cho tứ diện ABCD. Chứng minh rằng AB vuông góc với CD khi và chỉ khi
\(A{C^2} + B{{\rm{D}}^2} = A{{\rm{D}}^2} + B{C^2}\)

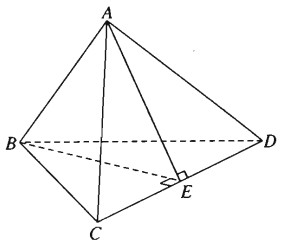
Giả sử AB⊥CD ta phải chứng minh \(A{C^2} + B{{\rm{D}}^2} = A{{\rm{D}}^2} + B{C^2}\).
Thật vậy, kẻ BE⊥CD tại E, do AB⊥CD ta suy ra CD⊥(ABE) nên CD⊥AE. Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ta có:
\(\eqalign{
& A{C^2} = A{{\rm{E}}^2} + C{E^2} \cr
& B{{\rm{D}}^2} = B{E^2} + E{{\rm{D}}^2} \cr
& B{C^2} = A{{\rm{E}}^2} + E{C^2} \cr
& {\rm{A}}{{\rm{D}}^2} = A{E^2} + E{{\rm{D}}^2} \cr} \)
Advertisements (Quảng cáo)
Từ đó ta suy ra \(A{C^2} + B{{\rm{D}}^2} = A{D^2} + B{C^2}\)
Ngược lại nếu tứ diện ABCD có \(A{C^2} + B{{\rm{D}}^2} = A{{\rm{D}}^2} + B{C^2}\) thì: \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2}\).
Nếu \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2} = {k^2}\) thì trong mặt phẳng (ACD) điểm A thuộc đường thẳng vuông góc với CD tại điểm H trên tia ID với I là trung điểm của CD sao cho \(I{H^2} = {{{k^2}} \over {2C{\rm{D}}}}\).
Tương tự điểm B thuộc đường thẳng vuông góc với CD cũng tại điểm H nói trên. Từ đó suy ra CD vuông góc với mặt phẳng (ABH) hay CD⊥AB.
Nếu \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2} = - {k^2}\) thì ta có và đưa về trường hợp xét như trên \(A{D^2} - A{C^2} = B{{\rm{D}}^2} - B{C^2} = - {k^2}\).
Chú ý.Từ kết quả của bài toán trên ta suy ra:
Tứ diện ABCD có các cặp cạnh đối diện vuông góc với nhau khi và chỉ khi \(A{B^2} + C{D^2} = A{C^2} + B{C^2}\).
