Advertisements (Quảng cáo)
Bài 6.4 trang 72 Sách bài tập (SBT) Vật lí 11 nâng cao
Mặt O nhìn theo phương vuông góc xuống đáy một chậu nước có chiết suất là \(n = {4 \over 3}\), bề dày lớp nước là 16 cm. Đáy chậu là một gương phẳng, nằm ngang. Mắt cách mặt nước 21 cm.
Hỏi ảnh của mắt cho bởi quang hệ cách mắt một khoảng bao nhiêu xentimet ?
Coi mắt O là vật. Ánh sáng từ O qua mặt phân cách không khí – nước cho ảnh trung gian \({O_1}\) (Hình 6.2G). Ta có :
\(HI = HO.\tan i = H{O_1}.{\mathop{\rm tanr}\nolimits} \)
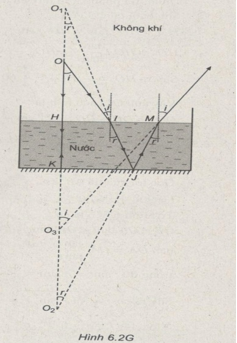
Vì nhìn theo phương vuông góc với mặt nước nên góc i nhỏ, do đó góc r cũng nhỏ.
Suy ra : \(\tan i \approx i,{\mathop{\rm tanr}\nolimits} \approx r\)
\({{H{O_1}} \over {HO}} = {{\tan i} \over {\tan r}} \approx {i \over r}\)
Mặt khác, sini = nsinr nên \({{\sin i} \over {{\mathop{\rm sinr}\nolimits} }} \approx {i \over r} = n\)
Vậy ta có : \({{H{O_1}} \over {HO}} = n\)
Suy ra : \(H{O_1} = n.HO = {4 \over 3}.21 = 28cm\)
Advertisements (Quảng cáo)
Ảnh \({O_1}\) là vật đối với gương phẳng, cho ảnh là \({O_2}\) đối xứng với \({O_1}\) qua gương. Ta có :
\(\eqalign{
& K{O_2} = K{O_1} = KH + H{O_1} \cr
& K{O_2} = 16cm + 28cm = 44cm \cr} \)
\({O_2}\) cách mặt thoáng của nước là :
\(H{O_2} = K{O_2} + HK = 44cm + 16cm \) \(= 60cm\)
Chùm tia phản xạ từ đáy chậu đi qua mặt phân cách nước – không khi cho ảnh cuối cùng là \({O_3}\).
\(HM = H{O_3}.\tan i = H{O_2}.{\mathop{\rm tanr}\nolimits} \)
\(H{O_3} = H{O_2}.{{\tan r} \over {{\mathop{\rm tani}\nolimits} }} \approx H{O_2}.{r \over i}\), với \({r \over i} \approx {1 \over n}\)
Suy ra \(H{O_3} = {1 \over n}.H{O_2} = {3 \over 4}.60 = 45cm.\)
Vậy ảnh \({O_3}\) cách mắt là :
\({\rm{O}}{{\rm{O}}_3} = OH + H{O_3} = 21cm + 45cm \) \(= 66cm\)