Advertisements (Quảng cáo)
Bài 6.5 trang 72 Sách bài tập (SBT) Vật lí 11 nâng cao
Một cái đinh được cắm vuông góc vào tâm O một tấm gỗ hình tròn có bán kính R = 5 cm. Tấm gỗ được thả nổi trên mặt thoáng của một chậu nước. Đầu A của đinh ở trong nước. Cho chiết suất của nước là \(n = {4 \over 3}\).
a) Cho chiều dài OA của đinh ở trong nước là 8,7 cm. Hỏi mắt ở trong không khí nhìn đầu đinh theo phương đi sát mép gỗ sẽ thấy đầu đinh ở cách mặt nước bao nhiêu xentimet ?
b) Cho chiều dài OA giảm dần. Tìm khoảng cách OA để mắt không còn nhìn thấy đầu A của đinh.
a) Ta có : \(\tan \alpha = {{OA} \over R} = {{8,7} \over 5} \approx 1,73\)
Suy ra: \(\alpha \approx {60^o}\)
Góc tới của tia AB là : \(i = {90^o} – \alpha = {30^o}\)
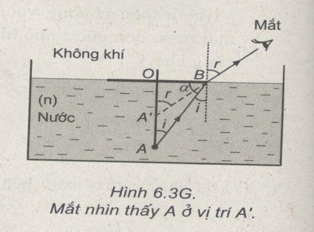
Từ Hình 6.3G, ta có :
\(OB = 0A.\tan i = OA’.tanr\) nên \(OA’ = OA.{{\tan i} \over {{\mathop{\rm t}\nolimits} {\rm{anr}}}}\)
Trong đó : \({\mathop{\rm s}\nolimits} {\rm{inr}} = n.\sin i = {4 \over 3}.\sin {30^o} = {2 \over 3}\)
Suy ra: \({\mathop{\rm cosr}\nolimits} = \sqrt {1 – {{\sin }^2}r} = {{\sqrt 5 } \over 3}\)
Vậy : \(\tan r = {2 \over {\sqrt 5 }}\)
(Có thể dùng bảng lượng giác để suy ra ngay giá trị của r và tanr)
Advertisements (Quảng cáo)
Mắt thấy đầu đinh A cách mặt nước một khoảng là :
\(OA’ = OA.{{\tan i} \over {\tan r}} = 8,7.{{\sqrt 5 } \over {2.\sqrt 3 }} \approx 5,62cm\)
Lưu ý : Trong thí nghiệm này, ảnh A’ sẽ không rõ vì góc tới i tương đối lớn, không thỏa mãn điều kiện góc nhỏ để có ảnh rõ.
b) Cho chiều dài AO giảm dần thì góc tới i sẽ tăng dần.
Khi \(i > {i_{gh}}\) (góc giới hạn) thì tia sáng sẽ phản xạ toàn phần, không có tia khúc xạ ló ra không khí. Khi đó, mắt không còn nhìn thấy đầu A của đinh nữa.
Ta có :
\(\eqalign{
& \sin {i_{gh}} = {1 \over n} = {3 \over 4} = 0,75 \cr
& \cos {i_{gh}} = \sqrt {1 – {{\sin }^2}{i_{gh}}} = {{\sqrt 7 } \over 4} \approx 0,66 \cr} \)
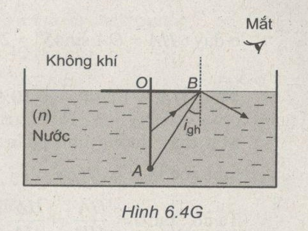
Từ Hình 6.4G, ta có :
\(OA = OB.\tan \left( {{\pi \over 2} – {i_{gh}}} \right)\), với OB = R = 5 cm.
Hay \(OA = OB.{{\cos {i_{gh}}} \over {\sin {i_{gh}}}} \approx 4,4cm\)
Vậy, nếu \(OA \le 4,4cm\) thì mắt sẽ không nhìn thấy đầu A của đinh.