
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA; I, J, K, L lần lượt là trung điểm của các đoạn thẳng SM, SN, SP, SQ.
a) Chứng minh rằng bốn điểm I, J, K, L đồng phẳng và tứ giác IJKL là hình bình hành.
b) Chứng minh rằng \(IK//BC\)
c) Xác định giao tuyến của hai mặt phẳng (IJKL) và (SBC)

Định lý Talet đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Đường trung bình của tam giác:
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Dấu hiệu nhận biết hình bình hành:
Hình có một cặp cạnh đối song song và bằng nhau là hình bình hành.

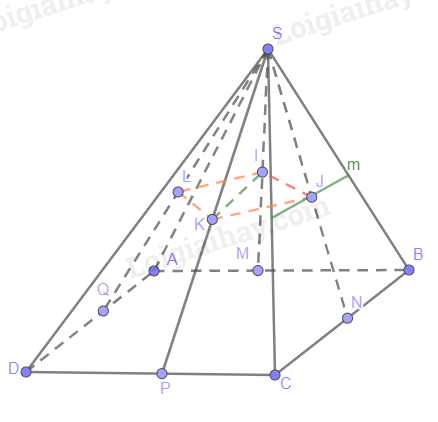
a) Tam giác ABC có M, N là trung điểm của AB, BC nên MN // AC (1)
Tam giác ACD có P, Q là trung điểm của CD, DA nên PQ // AC (2)
Tam giác SMN có I, J là trung điểm của SM, SN nên IJ // MN (3)
Advertisements (Quảng cáo)
Tam giác SPQ có L, K là trung điểm của SQ, SP nên LK // PQ (4)
Từ (1), (2), (3), (4) suy ra IJ // LK
Suy ra I, J, K, L đồng phẳng
Ta có:\(\frac{{MN}}{{AC}} = \frac{{QP}}{{AC}} = \frac{1}{2}\)
\(\frac{{{\rm{IJ}}}}{{MN}} = \frac{{LK}}{{PQ}} = \frac{1}{2}\)
Suy ra IJ = LK mà IJ // LK
Suy ra IJKL là hình bình hành
b) Ta có M, P lần lượt là trung điểm của AB, CD
Suy ra: MP // BC (1)
Tam giác SMP có: I, K là trung điểm của SM, SP
Suy ra: IK // MP (2)
Từ (1) và (2) suy ra: IK // BC
c) Ta có: J là giao điểm của hai mặt phẳng (IJKL) và (SBC)
mà IK // BC
Từ J kẻ Jm // BC
Suy ra Jm là giao tuyến của hai mặt phẳng (IJKL) và (SBC)
