Hoạt động 1
Cho hình lăng trụ tam giác có các mặt bên là hình chữ nhật ở Hình 80a, 80b. Hãy cho biết mỗi cạnh bên của lăng trụ đó có vuông góc với các mặt đáy hay không.
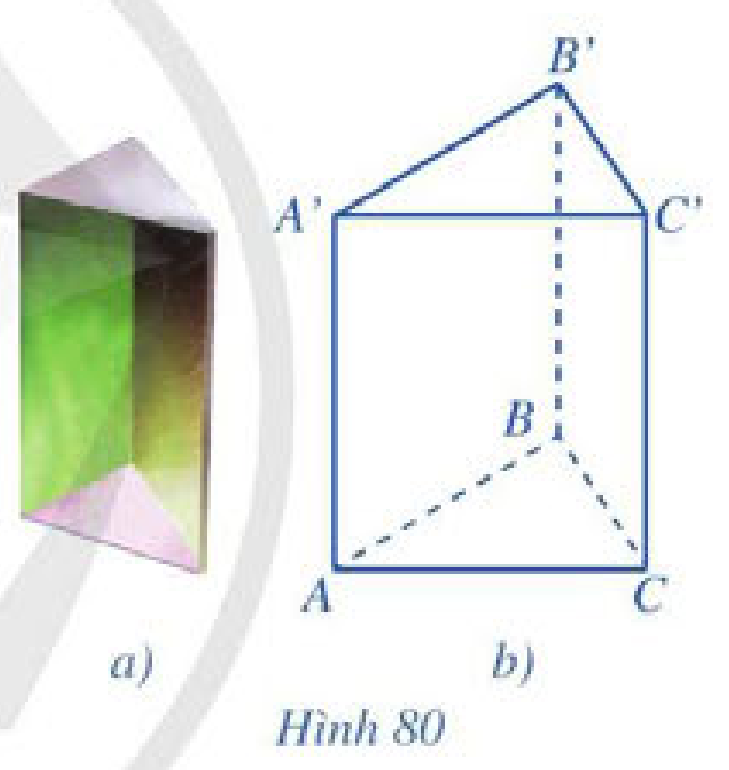

Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.

\(ABB’A’\) là hình chữ nhật \( \Rightarrow AA’ \bot AB\)
\(ACC’A’\) là hình chữ nhật \( \Rightarrow AA’ \bot AC\)
\(\left. \begin{array}{l} \Rightarrow AA’ \bot \left( {ABC} \right)\\AA’\parallel BB’\parallel CC’\end{array} \right\} \Rightarrow BB’ \bot \left( {ABC} \right),CC’ \bot \left( {ABC} \right)\)
Vậy các cạnh bên của lăng trụ đó vuông góc với các mặt đáy.
Advertisements (Quảng cáo)
Luyện tập 1
Cho hình lập phương có cạnh bằng \(a\). Tính độ dài đường chéo của hình lập phương đó.

Sử dụng định lí Pitago.`

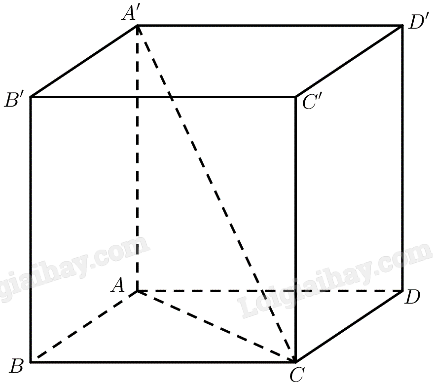
\(\Delta ABC\) vuông tại \(B \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(\Delta AA’C\) vuông tại \(A \Rightarrow A’C = \sqrt {AA{‘^2} + A{C^2}} = a\sqrt 3 \)
Vậy độ dài đường chéo của hình lập phương đó bằng \(a\sqrt 3 \).
