Hoạt động 1
Hình 2 biểu diễn các số hạng của dãy số \(\left( {{u_n}} \right),\) với \({u_n} = \frac{1}{n}\) trên hệ trục tọa độ.
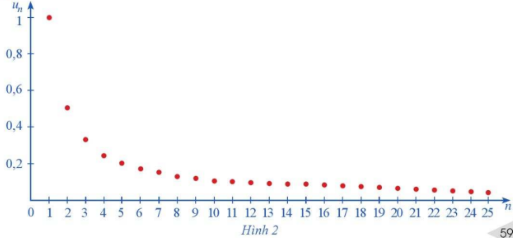
a) Nhận xét về sự thay đổi các giá trị \({u_n}\) khi n ngày càng lớn.
b) Hoàn thành bảng và trả lời câu hỏi sau:
Kể từ số hạng \({u_n}\) nào của dãy số thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,001? 0,0001?

Quan sát hình 2 và rút ra nhận xét.

a) Khi n ngày càng lớn thì các giá trị \({u_n}\) ngày càng giảm tiến dần về gần trục Ox.
b)
Kể từ số hạng \({u_{1001}}\) trở đi thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,001
Kể từ số hạng \({u_{10001}}\) trở đi thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,0001
Luyện tập, vận dụng 1
Chứng minh rằng:
a) \(\lim 0 = 0;\)
b) \(\lim \frac{1}{{\sqrt n }} = 0.\) \(\)
Advertisements (Quảng cáo)

Sử dụng định nghĩa dãy số có giới hạn 0.
Dãy số \(\left( {{u_n}} \right)\)có giới hạn 0 khi n dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi.

a) Vì \(\left| {{u_n}} \right| = \left| 0 \right| = 0 < 1\) nên theo định nghĩa dãy số có giới hạn 0 ta có \(\lim 0 = 0;\)
b) Vì \(0 < \left| {\frac{1}{{\sqrt n }}} \right| < 1\) nên theo định nghĩa dãy số có giới hạn 0 ta có \(\lim \frac{1}{{\sqrt n }} = 0.\)
Luyện tập, vận dụng 2
Chứng minh rằng \(\lim \frac{{ - 4n + 1}}{n} = - 4.\)

Sử dụng định nghĩa dãy số có giới hạn hữu hạn.
Dãy số \(\left( {{u_n}} \right)\)có giới hạn là số thực a khi n dần tới dương vô cực, nếu \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 0\), kí hiệu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\)hay \({u_n} \to a\)khi \(n \to + \infty \) hay \(\lim {u_n} = a\).

Vì \(\lim \left( {\frac{{ - 4n + 1}}{n} + 4} \right) = \lim \frac{1}{n} = 0\) nên \(\lim \frac{{ - 4n + 1}}{n} = - 4.\)
Luyện tập, vận dụng 3
Chứng minh rằng \(\lim {\left( {\frac{e}{\pi }} \right)^n} = 0.\)

Dãy số \(\left( {{u_n}} \right)\)có giới hạn 0 khi n dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dư mơng bé tùy ý , kể tử một số hạng nào đó trở đi.

Vì \(\left| {\frac{e}{\pi }} \right| < 1\) nên theo định nghĩa dãy số có giới hạn 0 ta có \(\lim {\left( {\frac{e}{\pi }} \right)^n} = 0.\)
