Hoạt động 2
Cho hai mặt phẳng phân biệt (P) và (Q). Mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và a, b cùng song song với mặt phẳng (Q) (Hình 61). Hai mặt phẳng (P) và (Q) có điểm chung hay không?


Quan sát hình vẽ

Hai mặt phẳng (P) và (Q) không có điểm chung
Luyện tập 2
Cho tứ diện ABCD. Các điểm M, N, P, I, J, K lần lượt là trung điểm của BC, CD, DB, AM, AN, AP. Chứng minh rằng (IJK) // (BCD).

Nếu mặt phẳng (P) chứa hai đường thẳng cắt nhau a, b và a,b cùng song song với mặt phẳng (Q) thì (P) song song với (Q)

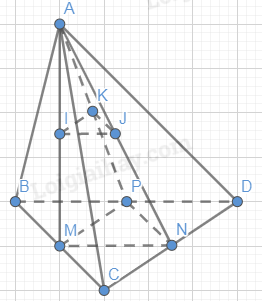
Tam giác AMP có: I, K là trung điểm AM, AP
Suy ra: IK // MP
Suy ra IK // (BCD) (1)
Tam giác ANP có: J, K là trung điểm AN, AP
Suy ra: JK // NP
Suy ra: JK // (BCD) (2)
Từ (1) và (2) suy ra: (IJK) // (BCD)
Hoạt động 3
Cho mặt phẳng (Q) và điểm M nằm ngoài mặt phẳng (Q).
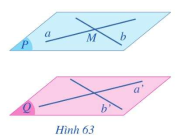
a) Trong mặt phẳng (Q) vẽ hai đường thẳng a’, b’ cắt nhau. Qua điểm M kẻ các đường thẳng a, và b lần lượt song song với a’, b’. Gọi (P) là mặt phẳng xác định bởi hai đường thẳng (cắt nhau) a và b (Hình 63). Mặt phẳng (P) có song song với mặt phẳng (Q) hay không?
b) Xét mặt phẳng (R) đi qua điểm M và song song với mặt phẳng (Q). Hai mặt phẳng (R) và (P) có trùng nhau hay không?

Advertisements (Quảng cáo)
Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.

a) Mặt phẳng (P) song song với mặt phẳng (Q)
b) Hai mặt phẳng (R) và (P) trùng nhau
Hoạt động 4
Cho hai mặt phẳng song song (P) và (Q). Mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a.
a) Mặt phẳng (R) có cắt mặt phẳng (Q) theo giao tuyến b, hãy nêu nhận xét về vị trí tương đối giữa hai giao tuyến a và b (Hình 64)
b) Trong trường hợp mặt phẳng (R) cắt mặt phẳng (Q) theo giao tuyến b, hãy nêu nhận xét về vị trí tương đối giữa hai giao tuyến a và b (Hình 64)
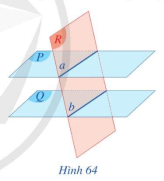

Cho hai mặt phẳng song song (P) và (Q). Nếu mặt phẳng (R) cắt mặt phẳng (P) thì cùng cắt mặt phẳng (Q) và hai giao tuyến của chúng song song với nhau

a) Hai giao tuyến a và b song song với nhau
b) Hai giao tuyến a và b song song với nhau
Luyện tập 3
Cho hai mặt phẳng (P) và (Q) song song với nhau. Đường thẳng a cắt hai mặt phẳng trên theo thứ tự tại A, B. Đường thẳng b song song với đường thẳng a và cắt hai mặt phẳng (P) và (Q) lần lượt tại A’, B’. Chứng minh rằng \(AB = A’B’\)

Hình tứ giác có hai cặp cạnh song song với nhau gọi là hình bình hành.

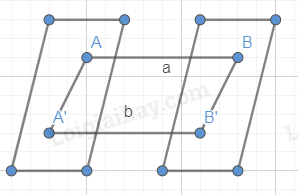
Ta có (P) // (Q)
Suy ra AA’ // BB’ (1)
Ta có a // b
Suy ra AB // A’B’ (2)
Từ (1) và (2) suy ra AA’B’B là hình bình hành
Do đó AB = A’B’
