Hoạt động 3
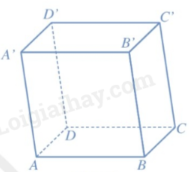
Vẽ hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành
Hình lăng trụ có đáy là hình bình hành là hình hộp
Luyện tập 2
Hãy liệt kê các đường chéo của hình hộp ABCD.A’B’C’D’ (Hình 73).
Đoạn thẳng nối hai đỉnh đối diện là đường chéo.
Các đường chéo của hình hộp ABCD.A’B’C’D’ là: A’C, AC’, D’B, DB’
Hoạt động 4
Nêu nhận xét gì về hai mặt phẳng chứa hai mặt đối diện của hình hộp
Quan sát hình hộp để rút ra nhận xét.
Hai mặt đối diện của hình hộp:
- Các mặt của hình hộp là các hình bình hành
- Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau
Luyện tập 3
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng bốn mặt phẳng (ABC’D’), (BCD’A’), (CDA’B’), (DAB’C’) cùng đi qua một điểm.
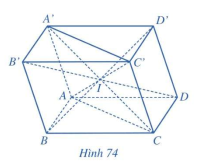
Trong hình hộp, tìm giao điểm của 4 đường chéo chính là giao điểm của 4 mặt phẳng (ABC’D’), (BCD’A’), (CDA’B’), (DAB’C’)
Theo ví dụ 3: Các đường chéo của hình hộp cắt nhau tại trung điểm mỗi đường
Gọi I là trung điểm của AC
Ta có: đường chéo hình hộp ABCD.A’B’C’D’ là A’C, AC’, D’B, DB’
Mà AC’, D’B thuộc (ABC’D’);
A’C, D’B thuộc (BCD’A’);
A’C, DB’ thuộc (CDA’B’)
AC’, DB’ thuộc (DAB’C’)
Do đó bốn mặt phẳng cùng đi qua điểm I (I là giao điểm của 4 đường chéo)