Áp dụng định lý Sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\) (a, b, c lần lượt là cạnh đối diện với góc A, B. Lời giải bài tập, câu hỏi - Bài 1.14 trang 19 SGK Toán 11 tập 1 - Cùng khám phá - Bài 3. Các phép biến đổi lượng giác. Cho tam giác có số đo các góc như Hình 1.29. Tính (cos A)...

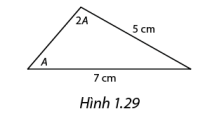
Cho tam giác có số đo các góc như Hình 1.29. Tính \(\cos A\).

Advertisements (Quảng cáo)
Áp dụng định lý Sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\) (a, b, c lần lượt là cạnh đối diện với góc A, B, C trong tam giác)

\(\begin{array}{l}\frac{5}{{\sin A}} = \frac{7}{{\sin 2A}}\\ \Leftrightarrow 5\sin 2A = 7\sin A\\ \Leftrightarrow 10\sin A\cos A = 7\sin A\\ \Leftrightarrow \cos A = \frac{7}{{10}}\end{array}\)
