Khoảng cách giữa 2 mặt phẳng song song là khoảng cách từ 1 điểm bất kì của mặt này đến mặt phẳng kia. Hướng dẫn giải - Bài 8.25 trang 79 SGK Toán 11 tập 2 - Cùng khám phá - Bài 4. Khoảng cách. Cho hình lăng trụ tam giác ABC. A’B’C’ có ABC là tam giác vuông cân tại A, A’ cách đều A, B...

Cho hình lăng trụ tam giác ABC.A’B’C’ có ABC là tam giác vuông cân tại A, A’ cách đều A, B, C và AA’ = AB = 2a. Tính khoảng cách giữa hai đáy của hình lăng trụ.

Khoảng cách giữa 2 mặt phẳng song song là khoảng cách từ 1 điểm bất kì của mặt này đến mặt phẳng kia.

Advertisements (Quảng cáo)
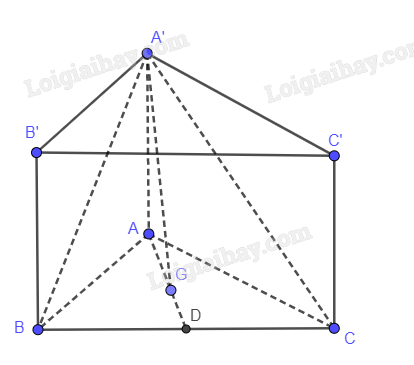
Gọi D là trung điểm BC, G là trọng tâm tam giác ABC
\(\begin{array}{l}AD = \sqrt 2 a\\ \Rightarrow AG = \frac{{2\sqrt 2 }}{3}a\end{array}\)
A’G vuông góc với (ABC) nên A’G vuông góc với AG
\(\begin{array}{l}A’G = \sqrt {AA{‘^2} - A{G^2}} = \sqrt {4{a^2} - {{\left( {\frac{{2\sqrt 2 }}{3}a} \right)}^2}} = \frac{{2\sqrt 7 }}{3}a\\\end{array}\)
