
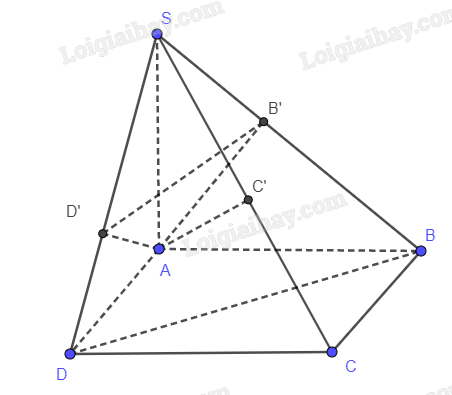
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD).
a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.
b) Mặt phẳng \(\left( \alpha \right)\) đi qua A và vuông góc với cạnh SC lần lượt cắt SB, SC, SD tại B’, C’, D’. Chứng minh B’D’ song song với BD và AB’vuông góc với SB.

a) Đường thẳng d vuông góc với 2 đường thẳng cắt nhau nằm trong (P) thì d vuông góc với (P).
b) Chứng minh a song song với b: Chứng minh a và b cùng vuông góc với c.
Chứng minh a vuông góc với b: Chứng minh a vuông góc với (P) chứa b.

a) SA vuông góc với (ABCD) nên SA vuông góc với AD, AB, BC, AD
Advertisements (Quảng cáo)
Suy ra tam giác SAD vuông tại A, tam giác SAB vuông tại A
Ta có: SA, AB vuông góc với BC nên (SAB) vuông góc với BC
Suy ra SB vuông góc với BC nên tam giác SBC vuông tại B
Có: SA, AD vuông góc với CD nên (SAD) vuông góc với CD
Suy ra SD vuông góc với CD nên tam giác SCD vuông tại D.
b) Vì B’, D’ thuộc \(\left( \alpha \right)\) và \(\left( \alpha \right)\) vuông góc với SC nên B’D’ vuông góc với SC (1)
Ta có: SA, AC vuông góc với BD nên (SAC) vuông góc với BD
Suy ra SC vuông góc với BD (2)
Từ (1) và (2) suy ra BD // B’D’
Ta có: (SAB) vuông góc với BC (cmt)
Mà: AB’ thuộc (SAB) nên AB’ vuông góc với BC.
