Hoạt động 1
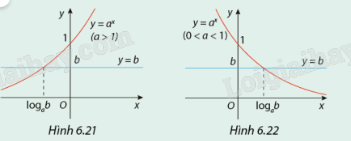
Quan sát các đồ thị ở trên và hãy biện luận theo b số giao điểm của đồ thị hàm số \(y = {a^x}\) và đường thẳng y = b.

Quan sát hình vẽ.

Ta có phương trình hoành độ giao điểm \({a^x} = b\)
Nếu b > 0 thì phương trình có nghiệm duy nhất là \(x = {\log _a}b\)
Nếu \(b \le 0\)thì phương trình vô nghiệm.
Luyện tập 1
Giải các phương trình:
Advertisements (Quảng cáo)
a) \({2.3^{x + 1}} - {6.3^{x - 1}} - {3^x} = 9\)
b) \(1,{5^{5x - 7}} = {\left( {\frac{2}{3}} \right)^{x + 1}}\)

Với \(a > 0,a \ne 1\), ta có: \({a^{A\left( x \right)}} = {a^{B\left( x \right)}} \Leftrightarrow A\left( x \right) = B\left( x \right)\,\)

a)
\(\begin{array}{l}{2.3^{x + 1}} - {6.3^{x - 1}} - {3^x} = 9\\ \Leftrightarrow {2.3^2}{.3^{x - 1}} - {6.3^{x - 1}} - {3.3^{x - 1}} = 9\\ \Leftrightarrow {3^{x - 1}}\left( {{{2.3}^2} - 6 - 3} \right) = 9\\ \Leftrightarrow {3^{x - 1}}.9 = 9\\ \Leftrightarrow {3^{x - 1}} = 1\\ \Leftrightarrow {3^{x - 1}} = {3^0}\\ \Leftrightarrow x - 1 = 0\\ \Leftrightarrow x = 1\end{array}\)
Vậy phương trình có nghiệm là x = 1.
b)
\(\begin{array}{l}1,{5^{5x - 7}} = {\left( {\frac{2}{3}} \right)^{x + 1}}\\ \Leftrightarrow {\left( {\frac{1}{{\frac{2}{3}}}} \right)^{5x - 7}} = {\left( {\frac{2}{3}} \right)^{x + 1}}\\ \Leftrightarrow \frac{1}{{{{\left( {\frac{2}{3}} \right)}^{5x - 7}}}} = {\left( {\frac{2}{3}} \right)^{x + 1}}\\ \Leftrightarrow {\left( {\frac{2}{3}} \right)^{x + 1}}.{\left( {\frac{2}{3}} \right)^{5x - 7}} = 1\\ \Leftrightarrow {\left( {\frac{2}{3}} \right)^{6x - 6}} = {\left( {\frac{2}{3}} \right)^0}\\ \Leftrightarrow 6x - 6 = 0\\ \Leftrightarrow x = 1\end{array}\)
Vậy phương trình có nghiệm x = 1.
