
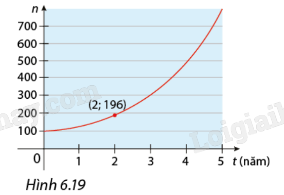
Lúc đầu trong ao có một số con ếch. Người ta ghi nhận số lượng ếch trong 5 năm đầu như Hình 6.19. Giả sử số lượng ếch tăng theo hàm số \(n\left( t \right) = C.{a^t}\).
a) Tính số lượng ếch lúc ban đầu.
b) Tìm hàm số biểu diễn số lượng ếch sau t năm kể từ khi chúng xuất hiện trong ao.
c) Dự đoán số lượng ếch sau 15 năm.

a) Số lượng ếch ban đầu là n khi t = 0.
b) Dựa vào các điểm thuộc đồ thị để tìm C, a.
Số lượng ếch mỗi năm bằng số lượng ếch ban đầu cộng với số lượng ếch tăng theo hàm số \(n\left( t \right) = C.{a^t}\).
Advertisements (Quảng cáo)
c) Thay t = 15 vào hàm số tìm được ở phần b.

a) Số lượng ếch ban đầu là 100 con.
b) Đồ thị hàm số đi qua 2 điểm (0; 100) và (2; 196). Ta có:
\(\left\{ \begin{array}{l}C.{a^0} = 100\\C.{a^2} = 196\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C = 100\\{a^2} = 1,96\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C = 100\\a = 1,4\end{array} \right.\)
\( \Rightarrow n\left( t \right) = 100.1,{4^t}\)
Vậy hàm số biểu diễn số lượng ếch sau t năm kể từ khi chúng xuất hiện trong ao là:
\(H\left( t \right) = 100 + 100.1,{4^t}\)
c) \(H\left( {15} \right) = 100 + 100.1,{4^{15}} \approx 15656\) (con).
