Hoạt động 3
a) Từ định nghĩa của \(\sin \alpha \)và \(\cos \alpha \), hãy tính \({\sin ^2}\alpha + {\cos ^2}\alpha \).
b) Từ định nghĩa của \(\tan \alpha \) và \(\cot \alpha \), hãy tính \(\tan \alpha .\cot \alpha \).




Luyện tập 4
Cường độ ánh sáng I đi xuyên qua một màn lọc ánh sáng được tính bởi công thức \(I = {I_m} - \frac{{{I_m}}}{{1 + {{\cot }^2}\alpha }}\), trong đó Im là cường độ ánh sáng đã chiếu lên màn lọc ánh sáng và là góc \(\alpha \) như trong Hình 1.21 (nguồn: http://www.vedantu.com/iit-jee/malus-law). Chứng minh rằng: \(I = {I_m}{\cos ^2}\alpha \).
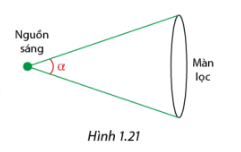

Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.

\(\begin{array}{l}I = {I_m} - \frac{{{I_m}}}{{1 + {{\cot }^2}\alpha }} = {I_m}\left( {1 - \frac{1}{{1 + {{\cot }^2}\alpha }}} \right) = {I_m}.\left( {1 - \frac{1}{{\frac{1}{{{{\sin }^2}\alpha }}}}} \right)\\ = {I_m}.\left( {1 - {{\sin }^2}\alpha } \right) = {I_m}.{\cos ^2}\alpha \end{array}\)
Hoạt động 4
a) Dựa vào Hình 1.22, hãy so sánh \(\cos \left( { - \alpha } \right)\) và \(\cos \left( \alpha \right)\); \(\sin \left( { - \alpha } \right)\) và \(\sin \left( \alpha \right)\).
b) Từ đó so sánh \(\tan \left( { - \alpha } \right)\) và \(\tan \left( \alpha \right)\); \(\cot \left( { - \alpha } \right)\) và \(\cot \left( \alpha \right)\).
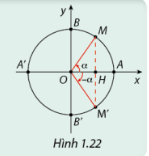

a) Quan sát hình vẽ.
b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.

a) Dựa vào Hình 1.22, ta thấy:
\(\cos \left( { - \alpha } \right)\) = \(\cos \left( \alpha \right)\)
\(\sin \left( { - \alpha } \right) = - \sin \left( \alpha \right)\)
b)
\(\begin{array}{l}\tan \left( { - \alpha } \right) = \frac{{\sin \left( { - \alpha } \right)}}{{\cos \left( { - \alpha } \right)}} = \frac{{ - \sin \alpha }}{{\cos \alpha }} = - \tan \alpha \\\cot \left( { - \alpha } \right) = \frac{{\cos \left( { - \alpha } \right)}}{{\sin \left( { - \alpha } \right)}} = \frac{{\cos \alpha }}{{ - \sin \alpha }} = - \cot \alpha \end{array}\)
Hoạt động 5
a) Dựa vào Hình 1.23, hãy so sánh \(\sin \left( {\pi - \alpha } \right)\) và \(\sin \left( \alpha \right)\); \(\cos \left( {\pi - \alpha } \right)\) và \(\cos \left( \alpha \right)\).
b) Từ đó so sánh \(\tan \left( {\pi - \alpha } \right)\) và \(\tan \left( \alpha \right)\); \(\cot \left( {\pi - \alpha } \right)\) và \(\cot \left( \alpha \right)\).
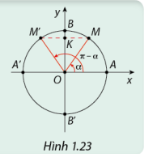

a) Quan sát hình vẽ.
b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.

a) Dựa vào Hình 1.23, ta thấy:
\(\sin \left( {\pi - \alpha } \right)\) = \(\sin \left( \alpha \right)\)
Advertisements (Quảng cáo)
\(\cos \left( {\pi - \alpha } \right) = - \cos \left( \alpha \right)\)
b) \(\tan \left( {\pi - \alpha } \right) = \frac{{\sin \left( {\pi - \alpha } \right)}}{{\cos \left( {\pi - \alpha } \right)}} = \frac{{\sin \alpha }}{{ - \cos \alpha }} = - \tan \alpha \)
\(\cot \left( {\pi - \alpha } \right) = \frac{1}{{\tan \left( {\pi - \alpha } \right)}} = \frac{1}{{ - \tan \alpha }} = - \cot \alpha \)
Hoạt động 6
a) Dựa vào Hình 1.24, hãy so sánh \(\sin \left( {\alpha + \pi } \right)\) và \(\sin \left( \alpha \right)\); \({\rm{cos}}\left( {\alpha + \pi } \right)\) và \(\cos \left( \alpha \right)\).
b) Từ đó so sánh \(\tan \left( {\alpha + \pi } \right)\) và \(\tan \left( \alpha \right)\); \(\cot \left( {\alpha + \pi } \right)\) và \(\cot \left( \alpha \right)\).
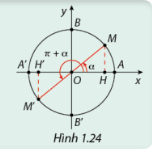

a) Quan sát hình vẽ.
b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.

a) Dựa vào Hình 1.24, ta thấy:
\(\sin \left( {\alpha + \pi } \right) = - \sin \alpha \)
\({\rm{cos}}\left( {\alpha + \pi } \right) = - \cos \alpha \)
b) \(\tan \left( {\alpha + \pi } \right) = \frac{{\sin \left( {\alpha + \pi } \right)}}{{\cos \left( {\alpha + \pi } \right)}} = \frac{{ - \sin \alpha }}{{ - \cos \alpha }} = \tan \alpha \)
\(\cot \left( {\alpha + \pi } \right) = \frac{{\cos \left( {\alpha + \pi } \right)}}{{\sin \left( {\alpha + \pi } \right)}} = \frac{{ - \cos \alpha }}{{ - \sin \alpha }} = \cot \alpha \)
Hoạt động 7
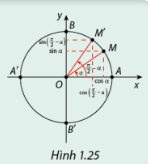
a) Dựa vào Hình 1.25, hãy so sánh \(\sin \left( {\frac{\pi }{2} - \alpha } \right)\) và \(\cos \left( \alpha \right)\); \({\rm{cos}}\left( {\frac{\pi }{2} - \alpha } \right)\) và \(\sin \left( \alpha \right)\).
b) Từ đó so sánh \(\tan \left( {\frac{\pi }{2} - \alpha } \right)\) và \(\cot \left( \alpha \right)\); \(\cot \left( {\frac{\pi }{2} - \alpha } \right)\) và \(\tan \left( \alpha \right)\).

a) Quan sát hình vẽ.
b) Áp dụng các hệ thức cơ bản giữa các giá trị lượng giác.

a) Dựa vào Hình 1.25, ta thấy:
\(\sin \left( {\frac{\pi }{2} - \alpha } \right)\) = \(\cos \left( \alpha \right)\)
\({\rm{cos}}\left( {\frac{\pi }{2} - \alpha } \right)\) = \(\sin \left( \alpha \right)\)
b) \(\tan \left( {\frac{\pi }{2} - \alpha } \right) = \frac{{\sin \left( {\frac{\pi }{2} - \alpha } \right)}}{{\cos \left( {\frac{\pi }{2} - \alpha } \right)}} = \frac{{\cos \alpha }}{{\sin \alpha }} = \cot \alpha \)
\(\cot \left( {\frac{\pi }{2} - \alpha } \right) = \frac{{\cos \left( {\frac{\pi }{2} - \alpha } \right)}}{{\sin \left( {\frac{\pi }{2} - \alpha } \right)}} = \frac{{\sin \alpha }}{{\cos \alpha }} = \tan \alpha \)
Luyện tập 5
Chứng minh giá trị của biểu thức sau không phụ thuộc \(\alpha \):
\(B = {\sin ^2}\left( {\alpha + \pi } \right) + {\sin ^2}\left( {\frac{\pi }{2} - \alpha } \right) + \cos \left( { - \alpha } \right) + \cos \left( {\pi - \alpha } \right)\)

Áp dụng các hệ thức giữa giá trị lượng giác của các góc lượng giác có liên quan đặc biệt.

\(\begin{array}{l}B = {\sin ^2}\left( {\alpha + \pi } \right) + {\sin ^2}\left( {\frac{\pi }{2} - \alpha } \right) + \cos \left( { - \alpha } \right) + \cos \left( {\pi - \alpha } \right)\\ \Leftrightarrow B = {\left( { - \sin \alpha } \right)^2} + {\cos ^2}\alpha + \cos \alpha - \cos \alpha \\ \Leftrightarrow B = {\sin ^2}\alpha + {\cos ^2}\alpha \\ \Leftrightarrow B = 1\end{array}\)
Vậy B không phụ thuộc \(\alpha \).
