Hoạt động 2
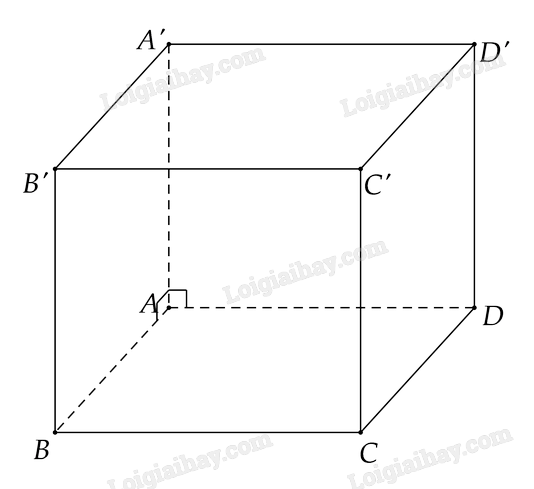
Cho hình hộp \(ABCD.A’B’C’D’\) có \(AA’ \bot AB\) và \(A’A \bot AD\) (Hình 8.8)
a) Mặt phẳng \(\left( {ABCD} \right)\) có vuông góc với \(A’A\) không? Vì sao?
b) Gọi \(\left( \alpha \right)\) là mặt phẳng qua \(A\) và vuông góc với \(A’A\). Hãy tìm giao tuyến của \(\left( \alpha \right)\) với các mặt phẳng \(\left( {AA’B’B} \right)\) và \(\left( {A’ADD’} \right)\). Từ đó tìm mối quan hệ giữa \(\left( \alpha \right)\) và mặt phẳng \(\left( {ABCD} \right)\)

a) Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
b) Tìm 2 điểm chung của 2 mặt phẳng là ta tìm được giao tuyến của chúng.

a) Vì \(\left\{ \begin{array}{l}AA’ \bot AB\\AA’ \bot AD\\AB \cap AD = \left\{ A \right\}\end{array} \right. \Rightarrow AA’ \bot \left( {ABCD} \right)\)
b) Vì \(\left( \alpha \right)\) đi qua \(A\) và vuông góc với \(AA’\)\( \Rightarrow \)\(\left( \alpha \right)\) trùng với \(\left( {ABCD} \right)\)
Do đó \(\left( \alpha \right) \cap \left( {AA’B’B} \right) = AB\)
\(\left( \alpha \right) \cap \left( {AA’D’D} \right) = AD\)
Luyện tập 2
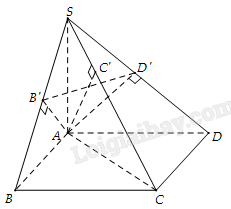
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật và \(SA\) vuông góc với đáy. Gọi \(B’,C’,D’\) lần lượt là hình chiếu của \(A\) trên các cạnh \(SB,SC,SD\). Chứng minh \(SC \bot \left( {AB’D’} \right)\) và \(AB’,AC’,AD’\) cùng nằm trên một mặt phẳng.

Chứng minh \(AB’ \bot \left( {SBC} \right) \Rightarrow AB’ \bot SC\)
Chứng minh \(AD’ \bot \left( {SCD} \right) \Rightarrow AD’ \bot SC\)
Chứng minh ba đường thẳng \(AB’,AC’,AD’\) cùng vuông góc với một đường thẳng

+) Ta có \(BC \bot AB\) (Vì \(ABCD\) là hình chữ nhật)
\(BC \bot SA\) vì \(SA \bot \left( {ABCD} \right)\)
Vì \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\)
Mà \(AB’ \subset \left( {SAB} \right) \Rightarrow AB’ \bot BC\)
Vì \(\left\{ \begin{array}{l}AB’ \bot SB\\AB’ \bot BC\end{array} \right. \Rightarrow AB’ \bot \left( {SBC} \right) \Rightarrow AB’ \bot SC\)
+) Ta có \(DC \bot AD\) (Vì \(ABCD\) là hình chữ nhật)
\(DC \bot SA\) vì \(SA \bot \left( {ABCD} \right)\)
Vì \(\left\{ \begin{array}{l}DC \bot AD\\DC \bot SA\end{array} \right. \Rightarrow DC \bot \left( {SAD} \right)\)
Mà \(AD’ \subset \left( {SAD} \right) \Rightarrow AD’ \bot DC\)
Vì \(\left\{ \begin{array}{l}AD’ \bot SD\\AD’ \bot DC\end{array} \right. \Rightarrow AD’ \bot \left( {SDC} \right) \Rightarrow AD’ \bot SC\)
Vì \(\left\{ \begin{array}{l}SC \bot AB’\\SC \bot AD’\end{array} \right. \Rightarrow SC \bot \left( {AB’D’} \right)\)
+) Ta có \(AB’,AC’,AD’\) cùng vuông góc với \(SC\) suy ra chúng cùng nằm trên mặt phẳng. Mà \(SC \bot \left( {AB’D’} \right)\) nên mặt phẳng đó là \(\left( {AB’D’} \right)\)
Hoạt động 3
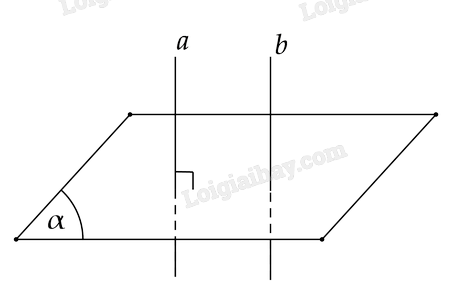
Cho hai đường thẳng \(a,b\) song song với nhau và mặt phẳng \(\left( \alpha \right)\) vuông góc với \(a\) (Hình 8.13). Hỏi \(\left( \alpha \right)\) có vuông góc với \(b\) không? Vì sao?

Sử dụng từ vuông góc đến song song

Ta có \(\left\{ \begin{array}{c}a//b\\a \bot \left( \alpha \right)\end{array} \right. \Rightarrow b \bot \left( \alpha \right)\)
Advertisements (Quảng cáo)
Luyện tập 3
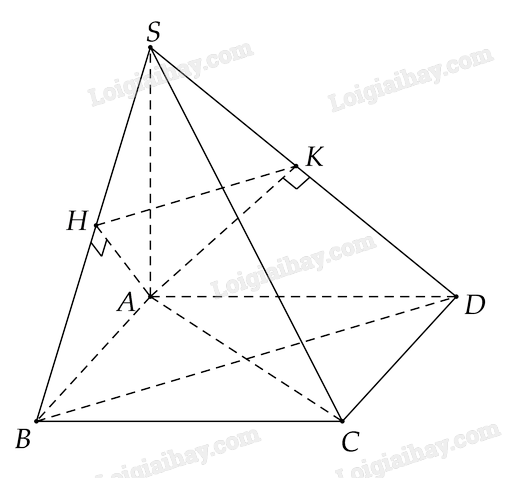
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(SA\) vuông góc với mặt phẳng đáy. Gọi \(H,K\) lần lượt là hình chiếu của \(A\) trên \(SB,SD\). Chứng minh \(HK \bot \left( {SAC} \right)\)

Chứng minh \(BD \bot \left( {SAC} \right)\) và \(HK//BD\). Từ đó suy ra \(HK \bot \left( {SAC} \right)\)

Ta có \(BD \bot AC\) (vì \(ABCD\) là hình vuông)
\(BD \bot SA\) vì \(SA \bot \left( {ABCD} \right)\)
Ta có \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\) \(\left( 1 \right)\)
Xét \(\Delta SAB\) có \(AH \bot SB\)\( \Rightarrow \frac{{SH}}{{SB}} = \frac{{SH.SB}}{{S{B^2}}} = \frac{{S{A^2}}}{{S{B^2}}}\)
Xét \(\Delta SAD\) có \(AK \bot SD\)\( \Rightarrow \frac{{SK}}{{SD}} = \frac{{SK.SD}}{{S{D^2}}} = \frac{{S{A^2}}}{{SD}}\)
Mà \(SB = SD\)\( \Rightarrow \frac{{SH}}{{SB}} = \frac{{SK}}{{SD}} \Rightarrow HK//BD\) (áp dụng định lý Ta – lét) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(HK \bot \left( {SAC} \right)\)
Luyện tập 4
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(O\) là giao điểm của \(AC\) và \(DB\), \(SA = SC\), \(SB = SD\). Gọi \(I,K\) lần lượt là trung điểm của \(AB\) và \(BC\). Mặt phẳng \(\left( \alpha \right)\) chứa \(IK\) và song song với \(SO\). Chứng minh \(\left( \alpha \right) \bot BD\)

Chứng minh \(\left( \alpha \right)//\left( {SAC} \right)\)
Chứng minh \(BD \bot \left( {SAC} \right)\) từ đó suy ra \(BD \bot \left( \alpha \right)\)

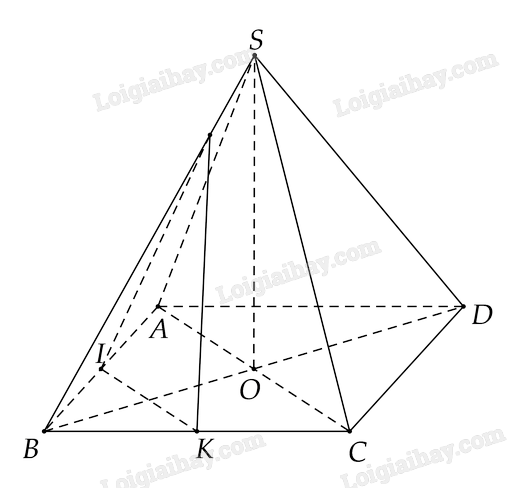
Ta có \(IK//AC\) vì \(IK\) là đường trung bình của \(\Delta SAC\)\(\left\{ \begin{array}{l}IK//AC\\IK \subset \left( \alpha \right)\end{array} \right. \Rightarrow AC//\left( \alpha \right)\)
Vì \(\left\{ \begin{array}{l}SO//\left( \alpha \right)\\AC//\left( \alpha \right)\end{array} \right. \Rightarrow \left( {SAC} \right)//\left( \alpha \right)\)
Vì \(ABCD\) là hình thoi tâm \(O\) nên \(AC \bot BD\) tại \(O\)
Xét \(\Delta SBD\) có \(SB = SD\) và \(O\) là trung điểm của \(BD\)\( \Rightarrow SO \bot BD\)
Vì \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\)
Mà \(\left( \alpha \right)//\left( {SAC} \right) \Rightarrow \left( \alpha \right) \bot BD\)
Luyện tập 5
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(SA \bot \left( {ABCD} \right)\). Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(B’\) là hình chiếu của \(A\) trên \(SB\), \(O’\) là hình chiếu của \(O\) trên \(SC\). Chứng minh \(AB’//\left( {O’BD} \right)\)

\(AB’//\left( {O’BD} \right)\)

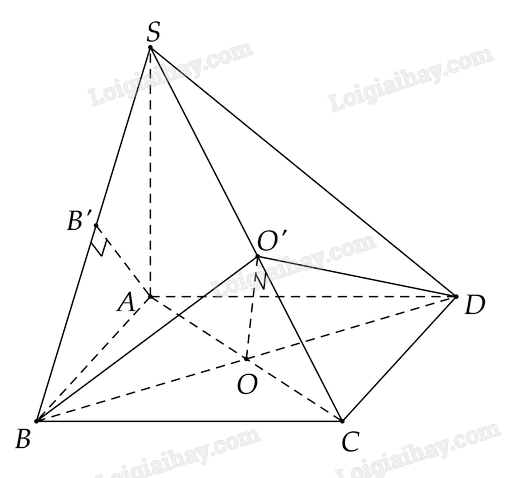
Ta có \(AC \bot BD\) (giả thiết)
Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BD\)
Vì \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\)
Vì \(\left\{ \begin{array}{l}OO’ \bot SC\,\,\left( {gt} \right)\\BD \bot SC\end{array} \right. \Rightarrow SC \bot \left( {O’BD} \right)\)
+) Ta có \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AB’\)
Ta có \(\left\{ \begin{array}{l}AB’ \bot BC\\AB’ \bot SB\end{array} \right. \Rightarrow AB’ \bot \left( {SBC} \right) \Rightarrow AB’ \bot SC\)
Vì \(\left\{ \begin{array}{l}AB’ \bot SC\\\left( {O’BD} \right) \bot SC\end{array} \right. \Rightarrow AB’//\left( {O’BD} \right)\)
