Hoạt động 4
Ở lớp dưới, ta đã biết số \(\sqrt 2 \) là một số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn: \(\sqrt 2 \) = 1,414213562... Gọi \({r_n}\) là số hữu tỉ được tạo thành từ n chữ số đầu tiên dùng để viết \(\sqrt 2 \) ở dạng thập phân, n = 1, 2,..., 10,...
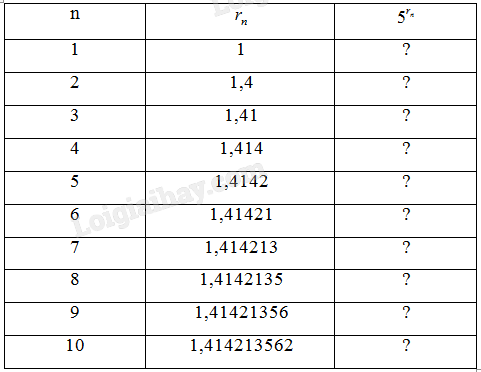
a) Sử dụng máy tính cầm tay, hãy tìm các số \({5^{{r_n}}}\) tương ứng (với 9 chữ số thập phân) cho mỗi dấu "?” trong bảng bên phải. Người ta chứng minh được rằng khi \(n \to + \infty \) thì dãy số (\({5^{{r_n}}}\)) dần đến một giới hạn mà ta kí hiệu là \({5^{\sqrt 2 }}\).
b) Sử dụng máy tính cầm tay, tính \({5^{\sqrt 2 }}\) (với 9 chữ số thập phân).

Sử dụng máy tính cầm tay.

a,
Advertisements (Quảng cáo)
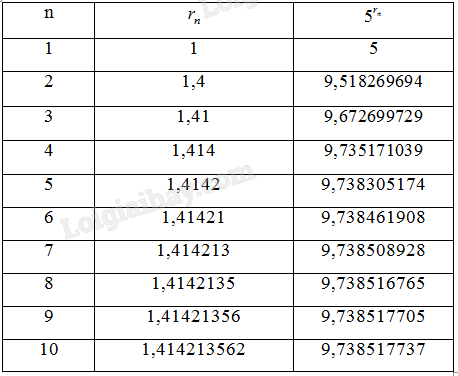
b) \({5^{\sqrt 2 }} \approx 9,738517742\)
Luyện tập 3
Rút gọn biểu thức \(\frac{{{{\left( {{a^{\sqrt 3 - 1}}} \right)}^{\sqrt 3 + 1}}}}{{{a^{\sqrt 5 - 3}}.{a^{4 - \sqrt 5 }}}}\,\,\left( {a > 0} \right)\).

Áp dụng: \({\left( {{a^n}} \right)^m} = {a^{n.m}};\,{a^n}.{a^m} = {a^{n + m}}\)

Ta có: \(\frac{{{{\left( {{a^{\sqrt 3 - 1}}} \right)}^{\sqrt 3 + 1}}}}{{{a^{\sqrt 5 - 3}}.{a^{4 - \sqrt 5 }}}} = \frac{{{a^{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}}}{{{a^{\sqrt 5 - 3 + 4 - \sqrt 5 }}}} = \frac{{{a^2}}}{a} = a\)
