Bài 2 trang 33 sách giáo khoa hình học lớp 11: Bài 8. Phép Đồng Dạng. Cho hình chữ nhật ABCD, AC và BD cắt nhau tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh hai hình thang JLKI và IHDC đồng dạng với nhau.Cho hình chữ nhật ABCD, AC và BD cắt nhau tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh hai hình thang JLKI và IHDC đồng dạng với nhau.
Bài 2. Cho hình chữ nhật \(ABCD, AC\) và \(BD\) cắt nhau tại \(I\). Gọi \(H, K, L\) và \(J\) lần lượt là trung điểm của \(AD, BC, KC\) và \(IC\). Chứng minh hai hình thang \(JLKI\) và \(IHDC\) đồng dạng với nhau.

Advertisements (Quảng cáo)
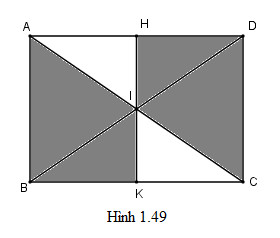
Phép vị tự tâm \(C\) tỉ số \(2\) biến hình thang \(JLKI\) thành hình thang \(IKBA\). Phép đối xứng tâm \(I\) biến hình thang \(IKBA\) thành hình thang \(IHDC\). Do đó hai hình thang \(JLKI\) và \(IHDC\) đồng dạng với nhau.
