Bài 3. Trong mặt phẳng \(Oxy\) cho điểm \(I (1;1)\) và đường trong tâm \(I\) bán kính \(2\). Viết phương trình của đường trong là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm \(O\), góc \( 45^{\circ}\) và phép vị tự tâm \(O\), tỉ số \( \sqrt{2}\).

Advertisements (Quảng cáo)
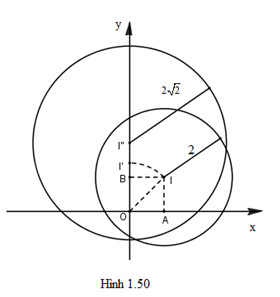
Phép quay tâm \(O\), góc \( 45^{\circ}\), biến \(I\) thành \(I'(0\);\( \sqrt{2}\)), phép vị tự tâm \(O\), tỉ số \( \sqrt{2}\) biến \(I’\) thành \(I” = (0; \)\( \sqrt{2}.\)\( \sqrt{2}\)) \(= (0;2)\). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm \(O\), góc \( 45^{\circ}\) và phép vị tự tâm \(O\), tỉ số \( \sqrt{2}\) biến đường tròn \((I;2)\) thành đường tròn \((I”;2\)\( \sqrt{2}\)). Phương trình của đường tròn đó là
\(x^{2}\) + \((y-2)^{2} = 8\).
