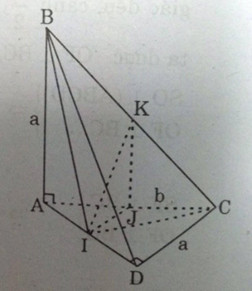
Bài 5. Tứ diện \(ABCD\) có hai mặt \(ABC\) và \(ADC\) nằm trong hai mặt phẳng vuông góc với nhau. Tam giác \(ABC\) vuông tại \(A\) có \(AB = a, AC = b\). Tam giác \(ADC\) vuông tại \(D\) có \(CD = a\).
a) Chứng minh các tam giác \(BAD\) và \(BDC\) đều là tam giác vuông
b) Gọi \(I\) và \(K\) lần lượt là trung điểm của \(AD\) và \(BC\). Chứng minh \(IK\) là đoạn vuông góc chung của hai đường thẳng \(AD\) và \(BC\).
 ‘
‘
a) \((ABC) ⊥ (ADC)\) mà hai mặt phẳng này giao nhau theo giao tuyến \(AC\).
Ta lại có \(BA ⊂ (ABC)\) và \(BA⊥ AC\) nên \(BA⊥(ADC)\)
\(BA⊥(ADC) ⇒ BA⊥AD ⇒ ΔBAD\) vuông tại \(A\)
\(\left. \matrix{
BA \bot (ADC) \hfill \cr
AD \bot DC \hfill \cr} \right\} \Rightarrow BD \bot DC\)
(Định lí 3 đường vuông góc)
\(⇒ ΔBDC\) vuông tại \(D\)
Advertisements (Quảng cáo)
b) Gọi \(J\) là trung điểm của \(AC\)
Ta có \(KJ//BA\)
Mà \(BA⊥(ADC) ⇒ KJ ⊥(ADC)\)
\( ⇒ KJ ⊥ AD\) (1)
Ta cũng có \(IJ//DC ⇒ IJ ⊥ AD\) (2)
Từ (1) và (2) suy ra: \(AD⊥(KIJ)\)
\(⇒ AD ⊥ IK\)
Ta lại có: \(ΔBAI = ΔCDI ⇒ IB = IC\)
\(⇒ ΔBIC\) cân đỉnh \(I ⇒ IK ⊥ BC\) (4)
Từ (3) và (4) suy ra \(IK\) là đoạn vuông góc chung của \(AD\) và \(BC\).
