ĐỀ 2 (45 phút)
Câu 1 (4 điểm) trang 23 sách bài tập (SBT) – Hình học 12
Cho khối tứ diện đều ABCD cạnh bằng a. Gọi A’, B’ , C’ , D’ lần lượt là trọng tâm của các tam giác BCD , CDA , DAB , ABC.
a) Chứng minh A’B’C’D’ cũng là một khối tứ diện đều.
b) Tính VA’B’C’D’ theo a.
Hướng dẫn làm bài
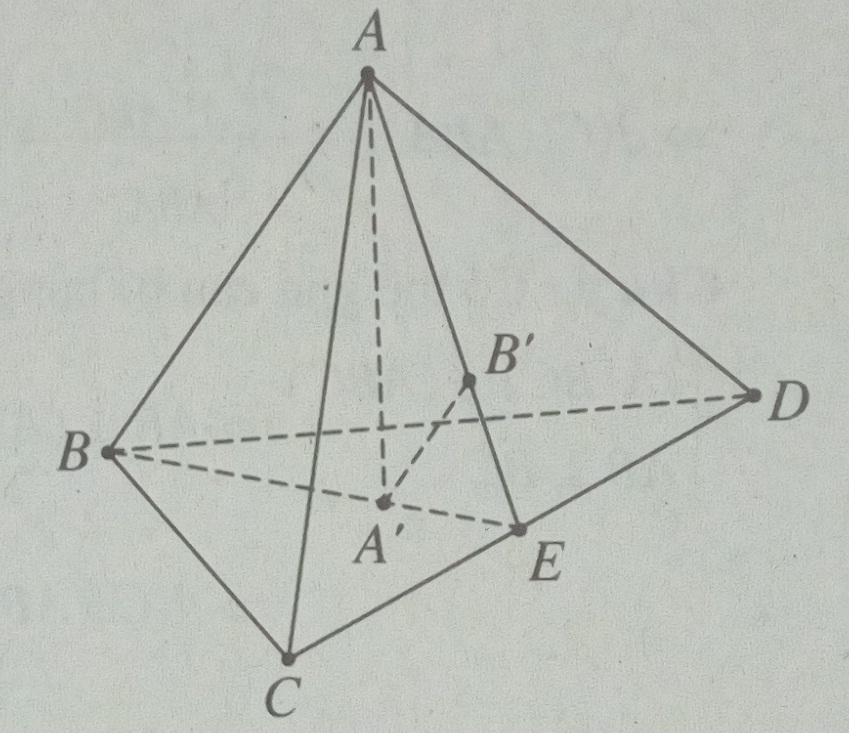
a) Gọi E là trung điểm của CD. Khi đó \({{EB’} \over {EA}} = {{EA’} \over {EB}}\)
Suy ra B’A’ // AB và \(B’A’ = {1 \over 3}AB = {1 \over 3}a\)
Tương tự các cạnh khác của tứ diện A’B’C’D’ cũng bằng \({1 \over 3}a\) nên A’B’C’D’ là một khối tứ diện đều.
b) Gọi H là hình chiếu của A lên mặt phẳng (BCD).
Vì AB = AC = AD nên HB = HC = HD. Suy ra: \(H \equiv A’\)
Ta có: \({\rm{AA}}’ = \sqrt {{a^2} - {{({a \over {\sqrt 3 }})}^2}} = {{a\sqrt 2 } \over {\sqrt 3 }}\)
\({V_{ABCD}} = {1 \over 3}{1 \over 2}{a^2}{{\sqrt 3 } \over 2}{{a\sqrt 2 } \over {\sqrt 3 }} = {{{a^3}\sqrt 2 } \over {12}}\)
Vì tứ diện A’B’C’D’ đồng dạng với tứ diện ABCD với tỉ số đồng dạng là \(k = {1 \over 3}\) , nên \({V_{A’B’C’D’}} = {1 \over {27}}{V_{ABCD}} = {{\sqrt 2 } \over {324}}{a^3}\)
Câu 2 (6 điểm) trang 23 sách bài tập (SBT) – Hình học 12
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác ABC vuông cân ở B, mặt phẳng (A’BC) vuông góc với mặt phẳng đáy, AB = 3a, AA’ = 5a ,\(\widehat {A’BC} = {60^0}\) .
Advertisements (Quảng cáo)
a) Tính thể tích khối lăng trụ ABC.A’B’C’
b) Tính khoảng cách từ C đến mặt phẳng (ABB’A’)
Hướng dẫn làm bài
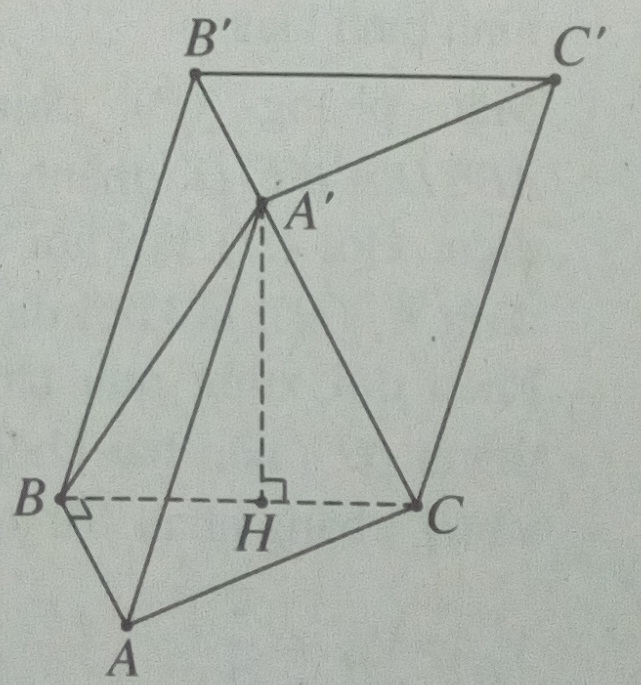
a) Gọi H là chân đường vuông góc kẻ từ A’ đến (ABC).
Vì \((A’BC) \bot (ABC)\) nên H thuộc đường thẳng BC. Vì \(AB \bot BH\) nên \(AB \bot BA’\).
Ta có: \(A’B = \sqrt {A'{A^2} - A{B^2}} = 4a\) ;
\(A’H = A’B\sin {60^0} = {{4a\sqrt 3 } \over 2} = 2\sqrt 3 a\) ;
\({V_{ABC.A’B’C’}} = {{9{a^2}} \over 2}2a\sqrt 3 = 9\sqrt 3 {a^3}\)
b) Ta có: \({V_{A’.ABC}} = {1 \over 3}{V_{ABC.A’B’C’}} = 3\sqrt 3 {a^3};\)
\({S_{ABA’}} = {1 \over 2}A’B.AB = {1 \over 2}4a.3a = 6{a^2}\)
Vì \({V_{A’.ABC}} = {V_{C.ABA’}} = {1 \over 3}{S_{ABA’}}.d(C,(ABA’))\)
\(\Rightarrow d(C,(ABA’)) = {{3{V_{A’.ABC}}} \over {{S_{ABA’}}}} = {{9\sqrt 3 {a^3}} \over {6{a^2}}} = {{3\sqrt 3 a} \over 2}\)
Chú ý: Có thể giải câu b) bằng cách khác như sau:
\(\left\{ {\matrix{{(A’BC) \bot (ABC)} \cr {AB \bot BC} \cr} } \right. \Rightarrow AB \bot (A’BC)\)
\(\Rightarrow (ABB’A’) \bot (A’BC)\)
\(\Rightarrow d(C,(ABB’A’)) = d(C,A’B) = BC\sin {60^0} = {{3a\sqrt 3 } \over 2}\)
