Câu hỏi/bài tập:

Trên mặt phẳng toạ độ \(Oxy\), vẽ nửa đường tròn tâm \(O\), bán kính \(r = 2\) nằm phía trên trục \(Ox\). Gọi \(D\) là hình phẳng giới hạn bởi nửa đường tròn, trục \(Ox\) và hai đường thẳng \(x = - 1\), \(x = 1\). Tính thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
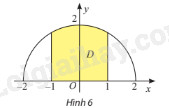

Viết phương trình nửa đường tròn tâm \(O\), bán kính \(r = 2\) nằm phía trên trục \(Ox\) là \(y = f\left( x \right)\).
Advertisements (Quảng cáo)
Hình phẳng \(D\) được giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = - 1\), \(x = 1\). Do đó, thể tích khối tròn xoay khi quay \(D\) quanh trục \(Ox\) là \(V = \pi \int\limits_{ - 1}^1 {{f^2}\left( x \right)dx} \).

Phương trình đường tròn tâm \(O\), bán kính \(r = 2\) là \({x^2} + {y^2} = {2^2} = 4\).
Do nửa đường tròn nằm phía trên trục \(Ox\), nên ta có \(y \ge 0\). Suy ra phương trình nửa đường tròn là \(y = \sqrt {4 - {x^2}} \).
Hình phẳng \(D\) được giới hạn bởi đồ thị hàm số \(y = \sqrt {4 - {x^2}} \), trục hoành và các đường thẳng \(x = - 1\), \(x = 1\). Do đó, thể tích khối tròn xoay khi quay \(D\) quanh trục \(Ox\) là
\(V = \pi \int\limits_{ - 1}^1 {{{\left( {\sqrt {4 - {x^2}} } \right)}^2}dx} = \pi \int\limits_{ - 1}^1 {\left( {4 - {x^2}} \right)dx} = \pi \left. {\left( {4x - \frac{{{x^3}}}{3}} \right)} \right|_{ - 1}^1 = \pi \left( {\frac{{11}}{3} - \frac{{ - 11}}{3}} \right) = \frac{{22\pi }}{3}\).
