Câu hỏi/bài tập:

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi G là trọng tâm của tam giác BC’D’.
a) Chứng minh rằng \(\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} } \right)\).
b) Tính theo a độ dài đoạn thẳng AG.

Sử dụng kiến thức về quy tắc hình hộp để giải bài toán: Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} = \overrightarrow {AC’} \)
Sử dụng kiến thức về độ dài của vectơ trong không gian để tính: Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\).

Advertisements (Quảng cáo)
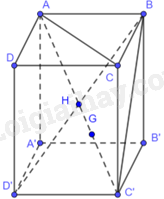
a) Gọi H là tâm của hình lập phương ABCD.A’B’C’D’. Khi đó, H là trung điểm của AC’. Do đó, \(\overrightarrow {AH} = \overrightarrow {HC’} = \frac{1}{2}\overrightarrow {AC’} \).
Vì G là trọng tâm của tam giác BC’D’ và C’H là đường trung tuyến của tam giác BC’D’ nên: \(\overrightarrow {HG} = \frac{1}{3}\overrightarrow {HC’} \).
Vì ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {AC’} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} \) (quy tắc hình hộp)
Ta có: \(\overrightarrow {AG} = \overrightarrow {AH} + \overrightarrow {HG} = \frac{1}{2}\overrightarrow {AC’} + \frac{1}{3}\overrightarrow {HC’} = \frac{1}{2}\overrightarrow {AC’} + \frac{1}{6}\overrightarrow {AC’} = \frac{2}{3}\overrightarrow {AC’} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} } \right)\)
b) Theo phần a ta có: \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AC’} \) nên \(AG = \frac{2}{3}AC’\)
Tam giác ACD vuông tại D nên \(AC = \sqrt {A{D^2} + D{C^2}} = a\sqrt 2 \)
Tam giác ACC’ vuông tại C nên \(AC’ = \sqrt {A{C^2} + CC{‘^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \)
Do đó, \(AG = \frac{2}{3}.a\sqrt 3 = \frac{{2a\sqrt 3 }}{3}\)
