Bài 10. Không tìm nguyên hàm hãy tính các tích phân sau:
a) \(\int\limits_{ - 2}^4 {\left( {{x \over 2} + 3} \right)dx} ;\) \(b)\,\int\limits_{ - 1}^2 {\left| x \right|} dx\)
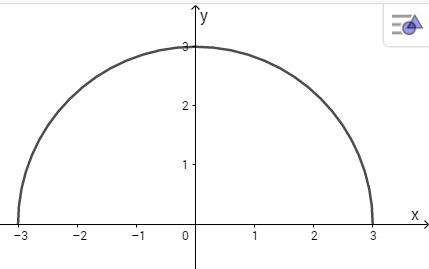
c) \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} } dx\)
Hướng dẫn: Áp dụng định lí 1.

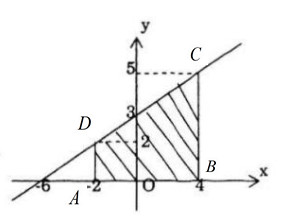
a) Tích phân đó bằng diện tích hình thang ABCD với cạnh nghiêng là đường thẳng \(y = {x \over 2} + 3.\) Diện tích đó là \(\left( {2 + 5} \right){6 \over 2} = 21.\) vậy \(\int\limits_{ - 2}^4 {\left( {{x \over 2} + 3} \right)dx = 21} .\)
Advertisements (Quảng cáo)
b)
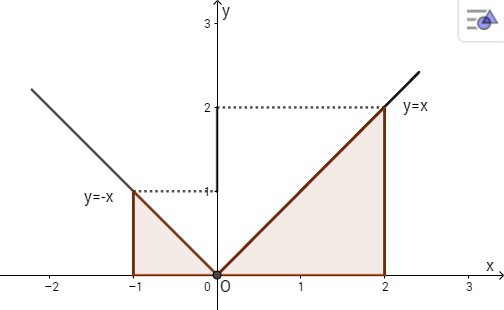
Từ hình trên ta thấy hình A gồm 2 tam giác. Do đó tích phân bằng diện tích của A và là \({1 \over 2}.1.1 + {1 \over 2}2.2 = 0,5 + 2 = 2,5\)
Vậy \(\int\limits_{ - 1}^2 {\left| x \right|} dx = {5 \over 2}\).
c) Tích phân bằng diện tích nửa đường tròn \({x^2} + {y^2} = 9\)(hình). Đây là đường tròn tâm là gốc tọa độ bán kính là 3. Do đó diện tích nửa dường tròn là \(9{\pi \over 2} = 4,5\pi .\)
Vậy \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} } dx = 4,5\pi \)