a) Tâm các mặt của một khối lập phương là các đỉnh của một khối tám mặt đều ;
b) Tâm cảc mặt của một khối tám mặt đều là các đỉnh của một khối lập phương.. Bài 14 trang 20 SGK Hình học 12 Nâng cao - Bài 3. Phép vị tự và sự đồng dạng của các khối đa diện. Các khối đa diện đều
Bài 14. Chứng minh rằng :
a) Tâm các mặt của một khối lập phương là các đỉnh của một khối tám mặt đều ;
b) Tâm cảc mặt của một khối tám mặt đều là các đỉnh của một khối lập phương.

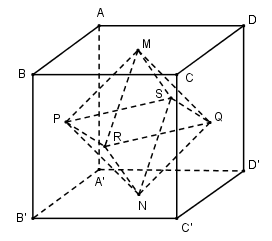
a) Gọi \(M, N, P, Q, R, S\) lần lượt là tâm của các mặt \(ABCD, A’B’C’D’, ABB’A’, CDD’C’, BCC’B’, ADD’A’\) của khối lập phương \(ABCD.A’B’C’D’\). Khi đó tám tam giác \(MPR, MRQ, MQS, MSP, NPR, NRQ, NQS, NSP\) là những tam giác đều, chúng làm thành khối đa diện với các đỉnh là \(M, N, P, Q, R, S\) mà mỗi đỉnh có \(4\) cạnh. Vậy đó là khối tám mặt đều.
Advertisements (Quảng cáo)
b) Cho khối tám mặt đều \(SABCDS’\). Gọi \(M, N, P, Q, M’, N’, P’, Q’\) lần lượt là trọng tâm của các mặt \(SAB, SBC, SCD, SAD, S’AB, S’BC, S’CD, S’DA\) thì các tứ giác \(MNPQ, M’N’P’Q’, MNN’M’, PQQ’P’, NPP’N’, MQQ’M’\) đều là hình vuông và mỗi đỉnh \(M, N, P, Q, M’, N’, P’, Q’\) đều là đỉnh chung của 3 cạnh.
Vậy \(MNPQ.M’N’P’Q’\) là khối lập phương.
Chú ý: Giả sử cạnh của khối tám mặt đều là \(a\) thì khối lập phương \(MNPQ.M’N’P’Q’\) là \({2 \over 3}{{a\sqrt 2 } \over 2} = {{a\sqrt 2 } \over 3}\)
