Chứng minh rằng các tiếp tuyến của mặt cầu song song với một đường thẳng cố định luôn nằm trên một mặt trụ xác định.. Bài 14 trang 53 SGK Hình học 12 Nâng cao - Bài 3. Mặt trụ hình trụ và khối trụ
Bài 14. Chứng minh rằng các tiếp tuyến của mặt cầu song song với một đường thẳng cố định luôn nằm trên một mặt trụ xác định.

Advertisements (Quảng cáo)
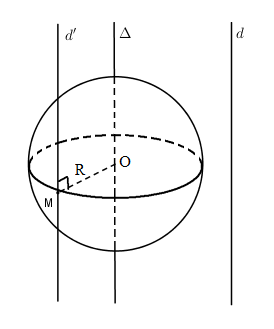
Cho mặt cầu \(S(O;R)\) và đường thẳng \(d\).
Gọi \(\Delta \) là đường thẳng đi qua \(O\) và song song với \(d\). Nếu \(d’\) là tiếp tuyến của mặt cầu và \(d’ // d\) thì \(d’\) cách \(\Delta \) một khoảng không đổi \(R\). Vậy \(d’\) nằm trên mặt trụ có trục \(\Delta \) và có bán kính bằng \(R\).
