Trong mỗi bài tập dưới đây, hãy chọn một phương án trong các phương án cho để được khẳng đinh đúng.
80. Hàm số \(f\left( x \right) = {{{x^3}} \over 3} - {{{x^2}} \over 2} - 6x + {3 \over 4}\)
(A) Đồng biến trên khoảng \(\left( { - 2;3} \right)\)
(B) Nghịch biến trên khoảng \(\left( { - 2;3} \right)\)
(C) Nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right)\)
(D) Đồng biến trên khoảng \(\left( { - 2; + \infty } \right)\)

\(f’\left( x \right) = {x^2} - x - 6;\,\,f’\left( x \right) = 0 \Leftrightarrow \left[ \matrix{
x = - 2 \hfill \cr
x = 3 \hfill \cr} \right.\)
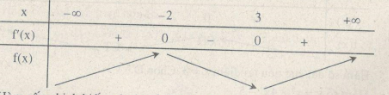
(B) Nghịch biến trên khoảng \(\left( { - 2;3} \right)\). Chọn (B).
81. Hàm số \(f\left( x \right) = 6{x^5} - 15{x^4} + 10{x^3} - 22\)
(A) Nghịch biến trên R;
(B) Đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\);
(C) Đồng biến trên khoảng R;
(D) Nghịch biến trên khoảng (0;1).

\(\eqalign{
& f’\left( x \right) = 30{x^4} - 60{x^3} + 30{x^2} = 30{x^2}\left( {{x^2} - 2x + 1} \right) = 30{x^2}{\left( {x - 1} \right)^2} \ge 0 \cr
& f’\left( x \right) = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 1 \hfill \cr} \right. \cr} \)
Hàm số đồng biến trên R. Chọn C.
82. Hàm số \(y = \sin x - x\)
(A) Đồng biến trên R.
(B) Đồng biến trên khoảng \(\left( { - \infty ;0} \right)\)
(C) Nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
(D) Nghịch biến trên R.

\(y’ = \cos x - 1 \le 0\,\,\,\,\,\forall x \in R\). Dấu bằng xảy ra khi và chỉ khi \(x = 2k\pi \)
Hàm số nghịch biến trên R. Chọn D.
83. Hàm số \(f\left( x \right) = {x^3} - 3{x^2} - 9x + 11\)
(A) Nhận điểm x = -1 làm điểm cực tiểu;
(B) Nhận điểm x = 3 làm điểm cực đại;
(C) Nhận điểm x = 1 làm điểm cực đại;
(D) Nhận điểm x = 3 làm điểm cực tiểu.

\(\eqalign{
& f’\left( x \right) = 3{x^2} - 6x - 9 \cr
& f’\left( x \right) = 0 \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr
x = 3 \hfill \cr} \right. \cr} \)
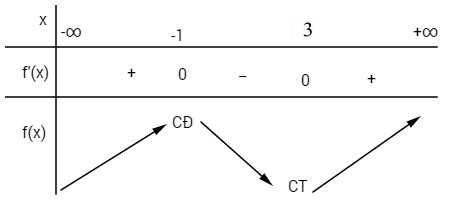
Hàm số đạt cực tiểu tại điểm x = 3. Chọn D.
84. Hàm số \(y = {x^4} - 4{x^3} - 5\)
(A) Nhận điểm x = 3 làm điểm cực tiểu.
(B) Nhận điểm x = 0 làm điểm cực đại
(C) Nhận điểm x = 3 làm điểm cực đại
(D) Nhận điểm x = 0 làm điểm cực tiểu.

\(\eqalign{
& y’ = 4{x^3} - 12{x^2} = 4{x^2}\left( {x - 3} \right) \cr
& y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 3 \hfill \cr} \right. \cr} \)
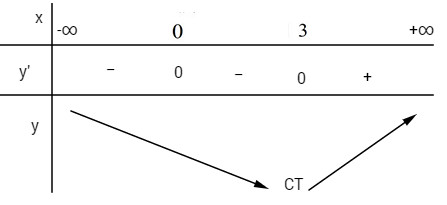
Hàm số đạt cực tiểu tại điểm x = 3. Chọn A.
85. Số điểm cực trị của hàm số \(y = {x^4} - 2{x^2} - 3\) là
(A) 0; (B) 1; (C) 3; (D) 2.

\(\eqalign{
& y’ = 4{x^3} - 4x = 4x\left( {{x^2} - 1} \right) \cr
& y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 1 \hfill \cr
x = - 1 \hfill \cr} \right. \cr} \)
Hàm số đạt 3 cực trị. Chọn C.
86. Số điểm cực trị của hàm số \(y = {{{x^2} - 3x + 6} \over {x - 1}}\) là
(A) 0; (B) 2; (C) 1; (D) 3.

\(y’ = 1 - {4 \over {{{\left( {x - 1} \right)}^2}}};\,y’ = 0 \Leftrightarrow {\left( {x - 1} \right)^2} = 4 \Leftrightarrow \left[ \matrix{
x = 3 \hfill \cr
x = - 1 \hfill \cr} \right.\)
Hàm số có 2 cực trị. Chọn B.
87.Hàm số f có đạo hàm là \(f’\left( x \right) = {x^2}{\left( {x + 1} \right)^2}\left( {2x - 1} \right)\). Số điểm cực trị của hàm số là
(A) 1; (B) 2; (C) 0; (D) 3.

Vì \({x^2}{\left( {x + 1} \right)^2} \ge 0\,\,\forall x \in R\) nên f’(x) chỉ đổi dấu khi x qua \({1 \over 2}\)
Hàm số có 1 cực trị. Chọn A.
88. Hàm số \(y = x - \sin 2x + 3\)
(A) Nhận điểm \(x = - {\pi \over 6}\) làm điểm cực tiểu.
(B) Nhận điểm \(x = {\pi \over 2}\) làm điểm cực đại.
(C) Nhận điểm \(x = - {\pi \over 6}\) làm điểm cực đại.
(D) Nhận điểm \(x = - {\pi \over 2}\) làm điểm cực tiểu.

\(y’ = 1 - 2\cos 2x;\,\,\,y” = 4\sin 2x\)
Ta có: \(y’\left( { - {\pi \over 6}} \right) = 0\,\,\,\text{và }\,\,y”\left( { - {\pi \over 6}} \right) < 0\)
Hàm số nhận điểm \(x = - {\pi \over 6}\) làm điểm cực đại.
CHọn (C)
89. Giá trị lớn nhất của hàm số \( - \sqrt {{3^2} + {4^2}} = - 5\) \(y = - 3\sqrt {1 - x} \) là:
(A) -3; (B) 1 (C) -1 (D) 0

\(y \le 0,\,\,\forall x \le 1\) và y(1) = 0
Nên \(\mathop {\max }\limits_{x \le 1} y = 0\)
Chọn D
90. Giá trị nhỏ nhất của hàm số \(y = 3\sin x - 4\cos x\) là:
(A) 3; (B) -5; (C) -4; (D) -3.

Ta có: \( - \sqrt {{a^2} + {b^2}} \le a\sin x + b\cos x \le \sqrt {{a^2} + {b^2}} \)
Giá trị nhỏ nhất của \(3\sin x - 4\cos x\) là \( - \sqrt {{3^2} + {4^2}} = - 5\)
Advertisements (Quảng cáo)
Chọn (B)
91. Giá trị lớn nhất của hàm số
\(\eqalign{
& f\left( x \right) = g\left( x \right) \Leftrightarrow 3 - {1 \over x} = 4{x^2} \Leftrightarrow 4{x^3} - 3x + 1 = 0 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow {\left( {2x - 1} \right)^2}\left( {x + 1} \right) = 0 \cr
& f’\left( {{1 \over 2}} \right) = g’\left( {{1 \over 2}} \right) = 0 \cr} \)
\(f\left( x \right) = 2{x^3} + 3{x^2} - 12x + 2\) trên đoạn \(\left[ { - 1;2} \right]\) là:
(A) 6; (B) 10; (C) 15; (D) 11.

\(\eqalign{
& f’\left( x \right) = 6{x^2} + 6x - 12 \cr
& f’\left( x \right) = 0 \Leftrightarrow \left[ \matrix{
x = 1 \in \left[ { - 1;2} \right] \hfill \cr
x = - 2 \in \left[ { - 1;2} \right] \hfill \cr} \right. \cr
& f\left( { - 1} \right) = 15;\,f\left( 1 \right) = - 5;\,f\left( 2 \right) = 6 \cr} \)
Vậy \(\mathop {\max }\limits_{x \in \left[ { - 1;2} \right]} f\left( x \right) = 15\)
92. Giá trị lớn nhất của hàm số \(f\left( x \right) = \sqrt { - {x^2} - 2x + 3} \) là:
(A) 2; (B) (C) 0; (D) 3.

TXĐ: \(D = \left[ { - 3;1} \right]\)
\(\eqalign{
& f’\left( x \right) = {{ - 2x - 2} \over {2\sqrt { - {x^2} - 2x + 3} }} = - {{x + 1} \over {\sqrt { - {x^2} - 2x + 3} }} \cr
& f’\left( 0 \right) \Leftrightarrow x = - 1\,\,\,\,\,f\left( { - 1} \right) = 2 \cr} \)
\(\mathop {\max }\limits_{x \in \left[ { - 3;1} \right]} f\left( x \right) = 2\). Chọn (A).
93. Gọi (C) là đồ thị của hàm số \(y = {{2{x^2} - 3x + 4} \over {2x + 1}}\)
(A) Đường thẳng x = -1 là tiệm cận đứng của (C).
(B) Đường thẳng x = 2x - 1 là tiệm cận đứng của (C).
(C) Đường thẳng x = x + 1 là tiệm cận đứng của (C).
(D) Đường thẳng x = x - 2 là tiệm cận đứng của (C).

\(y = x - 2 + {6 \over {2x + 1}}\)
Tiệm cận xiên : y = x- 2. Chọn (D).
94. Gọi (C) là đồ thị của hàm số \(y = {{{x^2} + 3} \over {3 + 5x - 2{x^2}}}\)
(A) Đường thẳng x = 1 là tiệm cận đứng của đồ thị (C).
(B) Đường thẳng \(x = - {1 \over 2}\) là tiệm cận đứng của đồ thị (C).
(C) Đường thẳng y = 1 là tiệm cận ngang của đồ thị (C).
(D) Đường thẳng x = -x +1 là tiệm cận xiên của đồ thị (C).

\(3 + 5x - 2{x^2} = 0 \Leftrightarrow \left[ \matrix{
x = - {1 \over 2} \hfill \cr
x = 3 \hfill \cr} \right.\)
Tiệm cận đứng \(x = - {1 \over 2}\). Chọn (B).
95. Gọi (C) là đồ thị của hàm số \(y = {{{x^2} + x + 2} \over { - 5{x^2} - 2x + 3}}\)
(A) Đường thẳng x = 2 là tiệm cận đứng của (C).
(B) Đường thẳng y = x -1 là tiệm cận xiên của (C).
(C) Đường thẳng \(y = - {1 \over 5}\) là tiệm cận ngang của (C).
(D) Đường thẳng \(y = - {1 \over 2}\) là tiệm cận ngang của (C).

\(\mathop {\lim }\limits_{x \to \pm \infty } y = {1 \over 5}\) . Tiệm cận ngang \(y = - {1 \over 5}\). Chọn (C).
96. Đồ thị của hàm số \(y = x + {1 \over {x - 1}}\)
(A) cắt đường thẳng y = 1 tại hai điểm;
(B) cắt đường thẳng y = 4 tại hai điểm;
(C) Tiếp xúc với đường thẳng y = 0.
(D) Không cắt đường thẳng y = -2.

\(x + {1 \over {x - 1}} = 4 \Leftrightarrow {x^2} - x + 1 = 4x - 4 \Leftrightarrow {x^2} - 5x + 5 = 0\,\,\,\left( 1 \right)\)
(1) Có hai nghiệm phân biệt. Chọn (B).
97. Xét phương trình \({x^3} + 3{x^2} = m\)
(A) Với m =5, phương trình đã có ba nghiệm;
(B) Với m = -1, phương trình có hai nghiệm.
(C) Với m =4, phương trình đã có ba nghiệm phân biệt;
(D) Với m =2, phương trình đã có ba nghiệm phân biệt

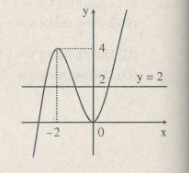
Vẽ đồ thị hàm số \(y = {x^3} + 3{x^2}\)
\(\eqalign{
& \,\,\,\,y’ = 3{x^2} + 6x;\,y’ = 0 \cr
& \Leftrightarrow \left[ \matrix{
x = - 2;\,\,y\left( { - 2} \right) = 4 \hfill \cr
x = 0;\,\,\,y\left( 0 \right) = 0 \hfill \cr} \right. \cr} \)
m =2: Phương trình có 3 nghiệm phân biệt.
Chọn (D).
98. Đồ thị hàm số \(y = {{x - 2} \over {2x + 1}}\)
(A) Nhận điểm \(\left( { - {1 \over 2};{1 \over 2}} \right)\) làm tâm đối xứng.
(B) Nhận điểm \(\left( { - {1 \over 2};2} \right)\) làm tâm đối xứng.
(C) Không có tâm đối xứng.
(D) Nhận điểm \(\left( {{1 \over 2};{1 \over 2}} \right)\) làm tâm đối xứng.

Tiệm cận đứng: \(x = - {1 \over 2}\); Tiệm cận ngang: \(y = {1 \over 2}\)
Giao điểm hai tiệm cận \(I\left( { - {1 \over 2};{1 \over 2}} \right)\) là tâm đối xứng của đồ thị hàm số.
Chọn (A).
99. Số giao điểm của hai đường cong \(y = {x^3} - {x^2} - 2x + 3\) và \(y = {x^2} - x + 1\) là:
(A) 0; (B) 1; (C) 3; (D) 2.

Hoành độ giao điểm của hai đường cong là nghiệm phương trình:
\(\eqalign{
& \,\,\,\,{x^3} - {x^2} - 2x + 3 = {x^2} - x + 1 \cr
& \Leftrightarrow {x^3} - 2{x^2} - x + 2 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - x - 2} \right) = 0 \cr
& \Leftrightarrow \left( {x - 1} \right)\left( {x + 1} \right)\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \matrix{
x = \pm 1 \hfill \cr
x = 2 \hfill \cr} \right.\,\,\,\,\,Chon\,(C) \cr} \)
100. Các đồ thị của hai hàm số \(y = 3 - {1 \over x}\) và \(y = 4{x^2}\) tiếp xúc với nhau tại điểm M có hoành độ là:
(A) x = -1; (B) x = 1; (C) x =2; (D) \(x = {1 \over 2}\)

\(\eqalign{
& f\left( x \right) = g\left( x \right) \Leftrightarrow 3 - {1 \over x} = 4{x^2} \Leftrightarrow 4{x^3} - 3x + 1 = 0 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow {\left( {2x - 1} \right)^2}\left( {x + 1} \right) = 0 \cr
& f’\left( {{1 \over 2}} \right) = g’\left( {{1 \over 2}} \right) = 0 \cr} \)
Chọn (D).
