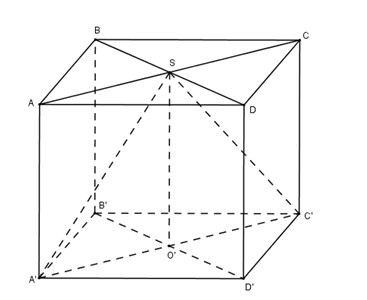
Bài 8. Cho hình lập phương \(ABCD.A’B’C’D’\) có cạnh bằng \(a\). Một hình nón có đỉnh là tâm của hình vuông \(ABCD\) và có đường tròn đáy ngoại tiếp hình vuông \(A’B’C’D’\). Diện tích xung quanh của hình nón đó là:
(A) \({{\pi {a^2}\sqrt 3 } \over 3}\) (B) \({{\pi {a^2}\sqrt 2 } \over 2}\)
(C) \({{\pi {a^2}\sqrt 3 } \over 2}\) (D) \({{\pi {a^2}\sqrt 6 } \over 2}\)

Advertisements (Quảng cáo)
Gọi \(O\) là tâm của hình vuông \( ABCD\) thì \( OA={{a\sqrt 2 } \over 2}\)
\(\eqalign{
& OA{‘^2} = AA{‘^2} + O{A^2} \cr
& \Rightarrow OA’ = {{a\sqrt 6 } \over 2} \cr} \)
Hình nón có đường sinh \(OA’\) và và bán kính đáy là: \({{a\sqrt 2 } \over 2}\) nên có diện tích xung quanh là:
\({S_{xq}} = \pi .{{a\sqrt 2 } \over 2}.{{a\sqrt 6 } \over 2} = {{\pi {a^2}\sqrt 3 } \over 2}\)
Chọn (C) \({{\pi {a^2}\sqrt 3 } \over 2}\).
