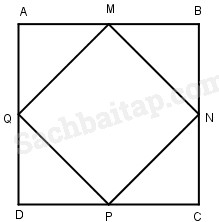
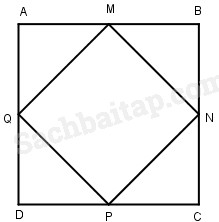
1. Cho hình vuông ABCD có cạnh 4cm. Trên các cạnh của hình vuông lấy lần lượt các trung điểm M, N, P, Q. Nối bốn điểm đó để được hình tứ giác MNPQ (xem hình vẽ). Tính tỉ số của diện tích hình tứ giác MNPQ và hình vuông ABCD.
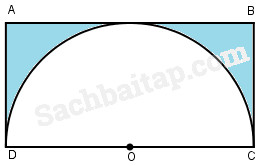
2. Cho hình bên gồm hình chữ nhật ABCD có AD = 2dm và một nửa hình tròn tâm O bán kính 2dm. Tính diện tích phần đã tô đậm của hình chữ nhật ABCD.
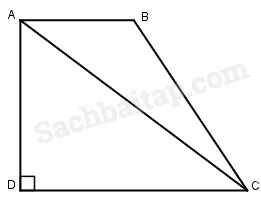
3. Cho hình thang vuông ABCD (xem hình vẽ) có AB = 20cm, AD = 30cm, DC = 40cm.
Nối A với C được hai hình tam giác là ABC và ADC. Tính :
a. Diện tích mỗi hình tam giác đó.
b. Tỉ số phần trăm của diện tích hình tam giác ABC và hình tam giác ADC.

1.
Bài giải
Vì M, N, P, Q lần lượt là trung điểm của AB, BC, CD và AD nên AM = MB = BN = NC = CP = PD = DQ = QA = 4 : 2 = 2cm
Diện tích hình vuông ABCD là :
4 ⨯ 4 = 16 (cm2)
Diện tích tam giác AMQ là :
\9{{2 \times 2} \over 2} = 2\,\left( {c{m^2}} \right)\)
Diện tích tứ giác MNPQ là :
16 – (4 ⨯ 2) = 8 (cm2)
Tỉ số của diện tích hình tứ giác MNPQ và hình vuông ABCD là :
\({8 \over {16}} = {1 \over 2}\)
Đáp số : \({1 \over 2}\)
2.
Advertisements (Quảng cáo)
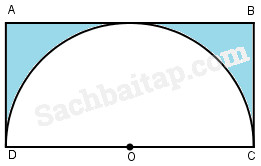
Bài giải
Diện tích hình chữ nhật ABCD là :
2 ⨯ 4 = 8 (dm2)
Diện tích nửa hình tròn tâm O là :
\({{2 \times 2 \times 3,14} \over 2} = 6,28\,\left( {d{m^2}} \right)\)
Diện tích phần đã tô đậm là :
8 – 6,28 = 1,72 (dm2)
Đáp số : 1,72dm2
3.
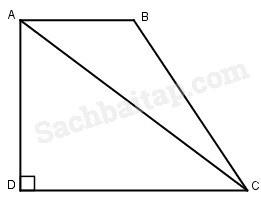
Bài giải
a. Diện tích hình thang ABCD là :
\({{\left( {20 + 40} \right) \times 30} \over 2} = 900\,\left( {c{m^2}} \right)\)
Diện tích tam giác ADC là :
\({{40 \times 30} \over 2} = 600\,\left( {c{m^2}} \right)\)
Diện tích tam giác ABC là :
900 – 600 = 300 (cm2)
b. Tỉ số phần trăm của diện tích tam giác ABC và hình tam giác ADC là :
\({{300} \over {600}} \times 100 = 50\% \)
Đáp số : a. Diện tích tam giác ABC : 300cm2
Diện tích tam giác ADC : 600cm2
b. %SABC = 50%
