
Cho tam giác ABC (AB < AC). Trên tia phân giác của góc A, lấy điểm E nằm trong tam giác ABC sao cho E cách đều hai cạnh AB, BC. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Điểm E không nằm trên tia phân giác của góc B.
b) \(\widehat {EBC} = \widehat {ECB}\).
c) Điểm E cách đều AB, BC, CA.
d) Điểm E nằm trên tia phân giác của góc C.

Sử dụng tính chấ ba đường phân giác của tam giác và chứng minh hai tam giác bằng nhau để xác định được các phát biểu đúng sai.

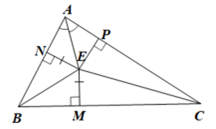
Gọi M, N, P lần lượt là hình chiếu của E trên BC, AB, AC.
Khi đó EM ⊥ BC, EN ⊥ AB, EP ⊥ AC và EN = EM.
• Xét ∆BNE và ∆BME có:
\(\widehat {{\rm{BNE}}} = \widehat {BME}\left( { = 90^\circ } \right)\)
EN = EM (giả thiết),
BE là cạnh chung
Do đó ∆BNE = ∆BME (cạnh huyền – cạnh góc vuông)
Suy ra \(\widehat {{\rm{NBE}}} = \widehat {MBE}\) (hai góc tương ứng)
Nên điểm E nằm trên tia phân giác của góc ABC.
Do đó phát biểu a là sai.
Advertisements (Quảng cáo)
•Vì AF là tia phân giác của góc BAC nên \(\widehat {{\rm{BAE}}} = \widehat {CAE}\)
Xét DANE và DAPE có:
\(\widehat {{\rm{ANE}}} = \widehat {APE}\left( { = 90^\circ } \right)\)
AE là cạnh chung,
\(\widehat {{\rm{NAE}}} = \widehat {PAE}\) (chứng minh trên).
Do đó ∆ANE = ∆APE (cạnh huyền – góc nhọn).
Suy ra EN = EP (hai cạnh tương ứng).
Mà EN = EM (giả thiết)
Nên EM = EN = EP hay điểm E cách đều ba cạnh AB, BC, CA.
Do đó phát biểu c là đúng.
• Xét hai ∆CPE và ∆CME có:
\(\widehat {CPE} = \widehat {CME}\left( { = 90^\circ } \right)\)
EP = EM (chứng mình trên),
CE là cạnh chung
Do đó ∆CPE = ∆CME (cạnh huyền – cạnh góc vuông)
Suy ra \(\widehat {{\rm{PCE}}} = \widehat {MCE}\) (hai góc tương ứng).
Nên điểm E nằm trên tia phân giác của góc ACB.
Do đó phát biểu d là đúng.
• Do AB < AC nên \(\widehat {ACB} < \widehat {ABC}\) (trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn).
Khi đó \(\widehat {EBC} = \frac{1}{2}\widehat {ABC} < \frac{1}{2}\widehat {ACB} = \widehat {ECB}.\)
Do đó phát biểu b là sai.
Vậy a, b là phát biểu sai; c, d là phát biểu đúng.
