
Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau thì các cặp góc đồng vị có được cũng bằng nhau”.
a) Hãy vẽ hình minh họa định lí trên.
b) Viết giả thiết và kết luận của định lí.
c) Hãy chứng minh định lí trên.

a) Hình vẽ minh họa:
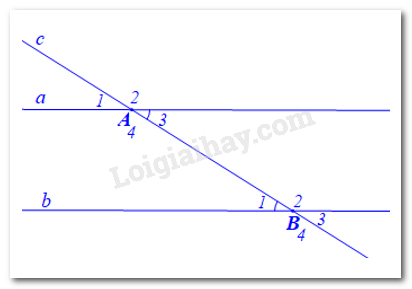
b) Viết giả thiết và kết luận bằng kí hiệu:
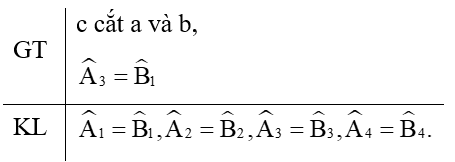
c) Chứng minh định lí:
• Vì \(\widehat {{A_1}}\) và \(\widehat {{A_3}}\) là hai góc đối đỉnh nên \(\widehat {{A_1}}\) = \(\widehat {{A_3}}\).
Advertisements (Quảng cáo)
Mà \(\widehat {{A_3}}\) = \(\widehat {{B_1}}\) (giả thiết)
Suy ra \(\widehat {{A_1}}\) = \(\widehat {{B_1}}\).
Chứng minh tương tự ta có: \(\widehat {{A_3}}\) = \(\widehat {{B_3}}\) (=\(\widehat {{B_1}}\))
• Lại có \(\widehat {{A_1}}\) và \(\widehat {{A_2}}\) là hai góc kề bù nên:
\(\widehat {{A_1}}\) + \(\widehat {{A_2}}\) =180°
Suy ra \(\widehat {{A_2}}\) =180°− \(\widehat {{A_1}}\) (1)
\(\widehat {{B_1}}\) và \(\widehat {{B_2}}\) là hai góc kề bù nên:
\(\widehat {{B_1}}\) + \(\widehat {{B_2}}\) =180°
Suy ra \(\widehat {{B_2}}\) =180°− \(\widehat {{B_1}}\) (2)
Mà \(\widehat {{A_1}}\) = \(\widehat {{B_1}}\) (3)
Từ (1), (2) và (3) suy ra \(\widehat {{A_2}}\) = \(\widehat {{B_2}}\).
Chứng minh tương tự ta cũng có \(\widehat {{A_4}}\) = \(\widehat {{B_4}}\).
Vậy định lí được chứng minh
