Giải Bài 5 trang 63 sách bài tập toán 7 - Chân trời sáng tạo - Bài 8: Tính chất ba đường cao của tam giác

Cho tam giác Abc cân tại A có góc A nhọn và H là trực tâm. Cho biết \(\widehat {BHC} = {150^o}\). Tính các góc của tam giác ABC.

- Áp dụng: tổng ba góc trong một tam giác bằng \({180^o}\) và đường cao trong tam giác để tính các số đo góc.

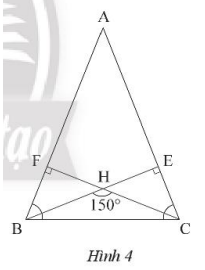
Vẽ hai đường cao BE và CF của tam giác ABC.
Advertisements (Quảng cáo)
Xét tam giác BHC ta có:
\(\widehat {HBC} + \widehat {HCB} = {180^o} - {150^o} = {30^o}\)
Xét hai tam giác vuông BCF và CBE ta có:
\(\widehat B + \widehat C = {180^o} - \left( {\widehat {HBC} + \widehat {HCB}} \right) = {180^o} - {30^o} = {150^o}\)
Do tam giác ABC cân tại A nên ta có:
\(\widehat B = \widehat C = \frac{{{{150}^o}}}{2} = {75^o}\)
\(\widehat {{A^{}}} = {180^o} - {150^o} = {30^o}\)
