Giải Bài 2 trang 65 sách bài tập toán 7 - Chân trời sáng tạo - Bài 9: Tính chất ba đường phân giác của tam giác

Cho tam giác ABC có \(\widehat {{A^{}}} = {42^o}\), ba đường phân giác đồng quy tại I. Tính số đo góc BIC.

Sử dụng tính chất tia phân giác của một góc để tính số đo góc.
Advertisements (Quảng cáo)

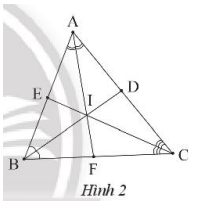
Ta có: \(\widehat B + \widehat C = {180^o} - \widehat {{A^{}}} = {180^o} - {62^o} = {118^o}\)
Do BI và CI là phân giác của góc B và góc C của tam giác ABC nên:
\(\widehat {IBC} + \widehat {ICB} = \frac{{\widehat B + \widehat C}}{2} = \frac{{{{118}^o}}}{2} = {59^o}\)
Suy ra: \(\widehat {BIC} = {180^o} - \left( {\widehat {IBC} + \widehat {ICB}} \right) = {180^o} - {59^o} = {121^o}\)
