Vẽ lại hình 3.20 vào vở.
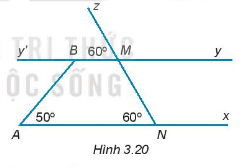
a) Giải thích tại sao \(Ax\parallel By.\)
b) Tính số đo góc \(ABy’\).
c) Tính số đo góc ABM.
a) Chỉ ra 2 góc đồng vị bằng nhau
b) Chỉ ra 2 góc so le trong bằng nhau
c) \(\widehat {ABM} + \widehat {ABy’} = {180^0}\)
a)
Ta có: \(\widehat {BMz} = \widehat {ANM}\left( { = {{60}^0}} \right)\)
Mà hai góc ở vị trí đồng vị nên \(Ax\parallel By\)(dấu hiệu nhận biết 2 đường thẳng song song).
b)
Ta có: \(Ax\parallel By\)\( \Rightarrow \widehat {ABy’} = \widehat {BAN}\)(2 góc so le trong)
Do đó \(\widehat {ABy’} = {50^0}\).
c)
Ta có: \(\widehat {ABM} + \widehat {ABy’} = {180^0}\) (hai góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {ABM} + {50^0} = {180^0}\\ \Rightarrow \widehat {ABM} = {180^0} - {50^0}\\ \Rightarrow \widehat {ABM} = {130^0}\end{array}\)