
Cho hình 3.36. Bên trong góc BOD vẽ tia Ox song song với AB. Biết \(\widehat B = {40^0};\widehat D = {70^0};\widehat {BOD} = {110^0}\).
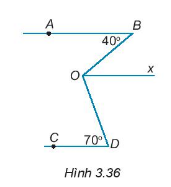
a) Tính số đo góc BOx.
b) Chứng minh \(Ox// CD;AB// CD.\)

a) Chỉ ra 2 góc so le trong bằng nhau.
b)
-Tính góc \(xOD\) ( \(\widehat {BOD} = \widehat {BOx} + \widehat {xOD}\))
-Chứng minh \(AB// CD\): cùng song song với Ox
Advertisements (Quảng cáo)

a)
Ta có: \(Ox// AB \Rightarrow \widehat {BOx} = \widehat B\) (2 góc so le trong). Mà \(\widehat B = {40^0}\) nên \(\widehat {BOx} =40^0\)
b)
Tia Ox nằm trong góc BOD nên
\(\begin{array}{l}\widehat {BOD} = \widehat {BOx} + \widehat {xOD}\\ \Rightarrow \widehat {xOD} = \widehat {BOD} - \widehat {BOx}\\ \Rightarrow \widehat {xOD} = {110^0} - {40^0}\\ \Rightarrow \widehat {xOD} = {70^0} \end{array}\)
Ta được: \(\widehat {xOD}= \widehat D(=70^0)\)
Mà 2 góc ở vị trí so le trong nên \(Ox// CD\) (Dấu hiệu nhận biết hai đường thẳng song song)
Ta có: \(\left\{ \begin{array}{l}AB// Ox\\CD// Ox\end{array} \right. \Rightarrow AB// CD.\) ( Tính chất)
