
Trong hình 3.37 có \(BE// AC,CF// AB\). Biết \(\widehat A = {80^0};\widehat {ABC} = {60^0}\).
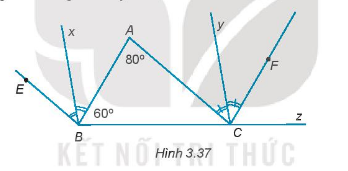
a) Chứng minh rằng \(\widehat {ABE} = \widehat {ACF}.\)
b) Tính số đo của các góc BCF và ACB.
c) Gọi Bx, Cy lần lượt là tia phân giác của các góc ABE và ACF. Chứng minh rằng \(Bx// Cy\).

a) Chứng minh 2 góc ABE và ACF cùng bằng góc A.
b)
- Tính góc FCz (chỉ ra cặp góc đồng vị).
- Tính góc BCF (Kề bù với góc FCz)
c)
- Tính \(\widehat{ABx}, \widehat{FCy}\).
- Chứng minh \(\widehat{xBC}= \widehat{yCz}\).
Advertisements (Quảng cáo)

a)
Ta có: \(BE// AC \Rightarrow \widehat {ABE} = \widehat A\) (cặp góc so le trong). Mà \(\widehat A= {80^0}\) nên \(\widehat {ABE} =80^0\)
\(AB//CF \Rightarrow \widehat {ACF} = \widehat A \) (cặp góc so le trong). Mà \(\widehat A= {80^0}\) nên \(\widehat {ACF} =80^0\)
\( \Rightarrow \widehat {ABE} = \widehat {ACF}.\)
b)
Ta có: \(AB// FC \Rightarrow \widehat {zCF} = \widehat {CBA}\) (cặp góc đồng vị). Mà \(\widehat {CBA}= {60^0}\) nên \(\widehat {zCF} =60^0\)
Lại có:\(\widehat {zCF} + \widehat {BCF} = {180^0}\) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow {60^0} + \widehat {BCF} = {180^0}\\ \Rightarrow \widehat {BCF} = {180^0} - {60^0}\\ \Rightarrow \widehat {BCF} = {120^0}\end{array}\)
Tia AC nằm trong góc BCF nên \(\widehat {ACB} = \widehat {BCF} - \widehat {ACF} = {120^0} - {80^0} = {40^0}\).
c)
Ta có: \(\widehat {EBx} = \widehat {xBA} = \widehat {ACy} = \widehat {yCF} = {40^0}\)
Nên \(\widehat {xBC} = \widehat {xBA} + \widehat {ABC} = {40^0} + {60^0} = {100^0}\)
\(\widehat {yCz} = \widehat {yCF} + \widehat {FCz} = {40^0} + {60^0} = {100^0}\)
\( \Rightarrow \widehat {xBC} = \widehat {yCz}\left( { = {{100}^0}} \right)\)
Mà 2 góc ở vị trí đồng vị nên \(Bx// Cy\) (Dấu hiệu nhận biết hai đường thẳng song song)
