
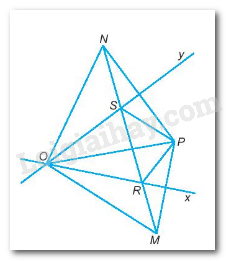
Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox là đường trung trực của đoạn thẳng PM, gọi N là điểm sao cho Oy là đường trung trực của đoạn thẳng PN. Đường thẳng MN cắt Ox tại R, cắt Oy tại S.Chứng minh tia PO là tia phân giác của góc RPS.

-O, R cùng nằm trên đường trung trực PM, chứng minh \(\widehat {OPR} = \widehat {OMR}\).
-O,S cùng nằm trên đường trung trực PN, chứng minh \(\widehat {OPS} = \widehat {ONS}\).

Ta có: O, R nằm trên đường trung trực của PM
\( \Rightarrow OP = OM;RP = RM\) (1)
Advertisements (Quảng cáo)
\( \Rightarrow \)Tam giác OPM cân tại O, tam giác RPM cân tại R.
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\widehat {OPM} = \widehat {OMP}\\\widehat {RPM} = \widehat {RMP}\end{array} \right.\\ \Rightarrow \widehat {OPR} = \widehat {OMR}\end{array}\)
Tương tự: O, S nằm trên đường trung trực của PN
\( \Rightarrow OP = ON;SP = SN\)(2)
\( \Rightarrow \)Tam giác OPN cân tại O, tam giác SPN cân tại S.
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\widehat {OPN} = \widehat {ONP}\\\widehat {SPN} = \widehat {SNP}\end{array} \right.\\ \Rightarrow \widehat {OPS} = \widehat {ONS}\end{array}\)
Từ (1) và (2) suy ra: OM = ON = OP hay OM = ON
\( \Rightarrow \)Tam giác OMN cân tại O
\( \Rightarrow \widehat {OMN} = \widehat {ONM}\)
Hay \(\widehat {OMR} = \widehat {ONS}\)
\( \Rightarrow \widehat {OPR} = \widehat {OPS}\) Vậy tia PO là tia phân giác của góc RPS.
