Giải bài 9.28 trang 81 SGK Toán lớp 7 tập 2 Kết nối tri thức với cuộc sống - Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
Xét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.
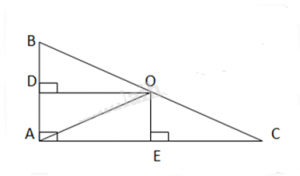
O cách đều 3 đỉnh của tam giác ABC
\( \Rightarrow \) \(OA = OB = OC\)
\( \Rightarrow \) \(\Delta OAB\) cân tại O.
Advertisements (Quảng cáo)
Giả sử O là trung điểm BC
\( \Rightarrow \widehat {OAB} = \widehat {OBA}\)
\(\Delta OAC\) cân tại O
\( \Rightarrow \widehat {OAC} = \widehat {OCA}\)
Xét tam giác ABC có
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\ \Rightarrow \widehat A + \widehat {OAB} + \widehat {OAC} = {180^0}\\ \Rightarrow \widehat A + \widehat A = {180^0}\\ \Rightarrow \widehat A = {90^0}\end{array}\)
Vậy nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.