
Cho đa thức \(F\left( x \right) = {x^4} - {x^3} - 6{x^2} + 15x - 9\)
a)Kiểm tra lại rằng x = 1 và x = -3 là hai nghiệm của F(x).
b)Tìm đa thức G(x) sao cho \(F\left( x \right) = \left( {x - 1} \right)\left( {x + 3} \right).G\left( x \right)\)

\(\begin{array}{l}F\left( x \right) = \left( {x - 1} \right)\left( {x + 3} \right).G\left( x \right)\\ \Rightarrow G\left( x \right) = F\left( x \right):\left[ {\left( {x - 1} \right)\left( {x + 3} \right)} \right]\\ \Rightarrow G\left( x \right) = \left( {{x^4} - {x^3} - 6{x^2} + 15x - 9} \right):\left( {{x^2} + 2x - 3} \right)\end{array}\)

Advertisements (Quảng cáo)
a)
Ta có:
\(\begin{array}{l}F\left( 1 \right) = {1^4} - {1^3} - {6.1^2} + 15.1 - 9 = 0\\F\left( 3 \right) = {3^4} - {3^3} - {6.3^2} + 15.3 - 9 = 0\end{array}\)
Vậy x = 1 và x = -3 là hai nghiệm của F(x).
b)
\(\begin{array}{l}F\left( x \right) = \left( {x - 1} \right)\left( {x + 3} \right).G\left( x \right)\\ \Rightarrow G\left( x \right) = F\left( x \right):\left[ {\left( {x - 1} \right)\left( {x + 3} \right)} \right]\\ \Rightarrow G\left( x \right) = \left( {{x^4} - {x^3} - 6{x^2} + 15x - 9} \right):\left( {{x^2} + 2x - 3} \right)\end{array}\)
Ta đặt tính chia:
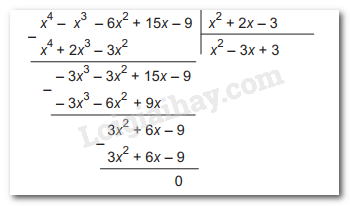
Vậy \(G\left( x \right) = {x^3} - 3x + 3\)
