
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Trên tia đối của tia MA lấy điểm D sao cho MD = MG. Chứng minh:
a) GA = GD;
b) \(\Delta MBG = \Delta MCD\);
c) \(CD = 2GN\).

a) Dựa vào tính chất ba đường trung tuyến trong tam giác.
b) Chứng minh hai tam giác này bằng nhau theo trường hợp c.g.c.
c) Dựa vào kết quả phần b) để chứng minh \(CD = 2GN\).

Advertisements (Quảng cáo)
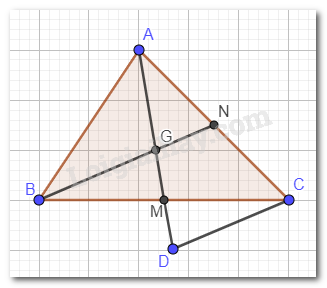
a) G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC.
Suy ra: \(AG = 2GM\). Mà trên tia đối của tia MA lấy điểm D sao cho MD = MG nên \(GD = 2GM\).
Vậy GA = GD(= 2GM).
b) Xét hai tam giác MBG và MCD có:
MB = MC (M là trung điểm cạnh BC)
\(\widehat {GMB} = \widehat {DMC}\)(đối đỉnh)
GM = GD.
Vậy \(\Delta MBG = \Delta MCD\)(c.g.c).
c) \(\Delta MBG = \Delta MCD\) nên BG = CD (2 cạnh tương ứng).
Mà G là trọng tâm tam giác ABC nên \(BG = 2GN\). Mà BG = CD nên \(CD = 2GN\).
