Bài 3 trang 84 Toán 7 Chân trời sáng tạo tập 2: Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia đối của HC lấy...

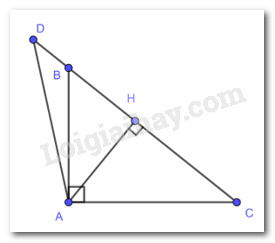
Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = HC.

a) Chứng minh rằng AD = AC.

b) Chứng minh rằng $\widehat {ADH} = \widehat {BAH}$

a) Ta chứng minh tam giác ACD cân tại A sau đó suy ra AC = AD

b) Ta chứng minh $\widehat {BAH} + \widehat {HAC} = {90^o} = \widehat {HAC} + \widehat {HCA}$ và $\widehat D = \widehat C$

a)      Xét $\Delta AHD$ và $\Delta AHC$ có :

AH chung

DH = HC ( C đối xứng D qua H)

$\widehat {AHD} = \widehat {AHC} = {90^o}$

$\Rightarrow \Delta AHD = \Delta AHC(c - g - c)$

$\Rightarrow AD = AC$(cạnh tương ứng)

$\Rightarrow \Delta ADC$cân tại A $\Rightarrow \widehat C = \widehat D$(góc tương ứng)(1)

b)      Ta có $\widehat {BAH} + \widehat {HAC} = {90^o}$và $\widehat {HCA} + \widehat {HAC} = {90^o}$

$\Rightarrow \widehat {BAH} = \widehat {HCA}$(2)

Từ (1) và (2) $\Rightarrow \widehat {ADH} = \widehat {BAH}$