
Cho tam giác ABC có đường trung tuyến BM bằng đường trung tuyến CN. Chứng minh rằng tam giác ABC cân.

- Ta chứng minh AB = AC bằng cách chứng minh 2 tam giác bằng nhau

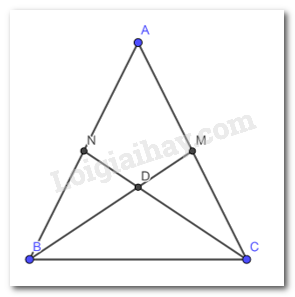
Gọi D là giao điểm của CN và BM
\( \Rightarrow \) D là trọng tâm tam giác ABC
\( \Rightarrow CD = \dfrac{2}{3}CN = BD = \dfrac{2}{3}BM\) ( do BM = CN )
\( \Rightarrow \) tam giác DBC cân tại D do BD = CD
Advertisements (Quảng cáo)
\( \Rightarrow \) \(\widehat {DBC} = \widehat {DCB}\)(2 góc đáy trong tam giác cân) (1)
Xét \(\Delta NDB\) và \(\Delta MDC\) có :
BD = CD
\(\widehat {NDB} = \widehat {MDC}\) (2 góc đối đỉnh)
ND = DM (do cùng \( = \dfrac{1}{3}CN = \dfrac{1}{3}BM\) (tính chất của trung trực đi qua trọng tâm tam giác ))
\( \Rightarrow \Delta NDB=\Delta MDC\) (c.g.c)
\( \Rightarrow \,\widehat {NBD} = \widehat {MCD}\)(2 góc tương ứng) (2)
Từ (1) và (2) \( \Rightarrow \widehat {ABC} = \widehat {ACB}\) do \(\widehat {ABC} = \widehat {NBD} + \widehat {DBC}\) và \(\widehat {ACB} = \widehat {MCD} + \widehat {DCB}\)
\( \Rightarrow \Delta ABC\) cân tại A (do 2 góc bằng nhau)
