
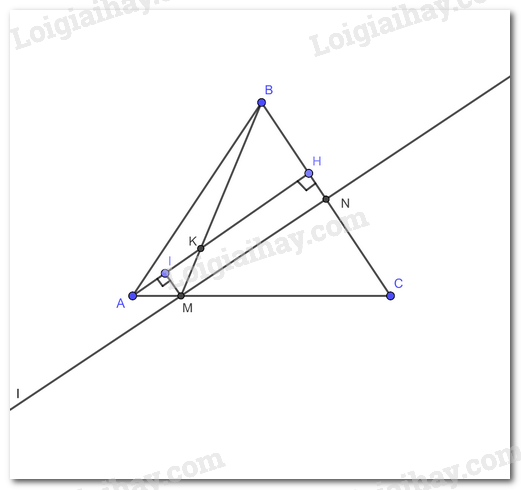
Cho tam giác nhọn ABC (AB < AC), vẽ đường cao AH. Đường trung trực của BC cắt AC tại M, cắt BC tại N.
a) Chứng minh rằng \(\widehat {BMN} = \widehat {HAC}\)
b) Kẻ \(MI \bot AH\)(I ∈ AH), gọi K là giao điểm của AH và BM. Chứng minh rằng I là trung điểm của AK.

a) Ta xét tam giác BMC cân tại M nên \(\widehat {MBC} = \widehat {MCB}\)
Nên \(\widehat {BMN} = \widehat {HAC} = {90^o} - \widehat {MBC} = {90^o} - \widehat {MBC}\)
b) Ta chứng minh I là trung điểm của AK do \(\Delta MAI = \Delta MKI\)(g-c-g)

a) Ta xét tam giác BMC cân tại M nên \(\widehat {MBC} = \widehat {MCB}\)
Nên \(\widehat {BMN} = \widehat {HAC} = {90^o} - \widehat {MBC} = {90^o} - \widehat {MBC}\)
b) Ta chứng minh I là trung điểm của AK do \(\Delta MAI = \Delta MKI\)(g-c-g)
Advertisements (Quảng cáo)
Lời giải :
a) Xét tam giác BMC cân tại M (Do M thuộc đường trung trực của BC nên MB = MC) có : \(\widehat {MBC} = \widehat {MCB}\)(góc tương ứng)
Mà \(\widehat {BMN} = {90^o} - \widehat {MBC}\)và \(\widehat {HAC} = {90^o} - \widehat {BCM}\)
\( \Rightarrow \)\(\widehat {BMN} = \widehat {HAC}\)
b) Ta có MN⫽AH (do cùng vuông góc với BC)
\( \Rightarrow \widehat {AKM} = \widehat {KMN}\)(2 góc so le trong)
Mà \(\widehat {BMN} = \widehat {HAC}\)( chứng minh a)
\( \Rightarrow \widehat {KAM} = \widehat {AKM}\)( do cùng =\(\widehat {BMN}\))
Xét \(\Delta MIA\) và \(\Delta MIK\)có :
IM cạnh chung
\(\widehat {KAM} = \widehat {AKM}\)
\(\widehat {AIM} = \widehat {MIK} = {90^o}\)
\( \Rightarrow \Delta MIA = \Delta MIK\)(cạnh góc vuông-góc nhọn)
\( \Rightarrow \)AI = IK (cạnh tương ứng)
\( \Rightarrow \)I là trung điểm AK
