Tính chất của tam giác cân trang 60, 61, 62 Toán 7 Chân trời sáng tạo tập 2...

HĐ 2

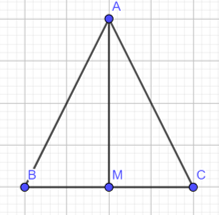
Cho tam giác ABC cân tại A (Hình 5). Gọi M là trung điểm cạnh BC. Nối A với M. Em hãy làm theo gợi ý sau để chứng minh $\widehat {ABC}$=$\widehat {ACB}$.

Xét $\Delta AMB$ và $\Delta AMC$có:

AB = ? (?)

MB = MC (?)

AM là cạnh ?

Vậy $\Delta AMB$ =$\Delta AMC$ (c.c.c)

Suy ra $\widehat {ABC}$=$\widehat {ACB}$

Dựa vào định nghĩa của tam giác cân là tam giác có 2 cạnh bằng nhau

Xét $\Delta AMB$ và $\Delta AMC$.có:

AB = AC ( do tam giác ABC cân tại A )

MB = MC ( do M là trung điểm BC )

AM là cạnh chung

=>$\Delta AMB$ =$\Delta AMC$ (c.c.c)

=>$\widehat {ABC}$=$\widehat {ACB}$( 2 góc tương ứng)

Thực hành 2

Tìm số đo các góc chưa biết của mỗi tam giác trong Hình 7.

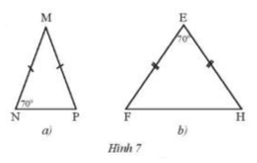
Dựa vào định lí 2 góc đáy của tam giác cân bằng nhau

a) Vì $\Delta MNP$ cân tại M ( theo giả thiết )

$\Rightarrow \widehat N = \widehat P = {70^o}$ ( 2 góc đáy của tam giác cân )

$\Rightarrow \widehat M = {180^o} - {2.70^o} = {40^o}$

b) Xét $\Delta EFH$ cân tại E

Theo định lí về tổng 3 góc trong tam giác ta có

$\Rightarrow \widehat E + \widehat F + \widehat H = {180^o}$

Mà $\widehat F = \widehat H$( tính chất tam giác cân )

$\Rightarrow \widehat F = \widehat H = {180^o} - \widehat E = ({180^o} - {70^o}):2 = {55^o}$

Vận dụng 1

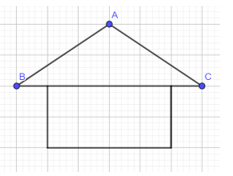
Trong hình mái nhà ở Hình 8, tính góc B và góc C, biết $\widehat A$= ${110^o}$.

Dựa vào tính chất 2 góc đáy của tam giác cân bằng nhau

Vì tổng số đo 3 góc trong tam giác là ${180^o}$

$\Rightarrow \widehat A + \widehat B + \widehat C = {180^o}$

Mà $\widehat B = \widehat C$$= ({180^o} - \widehat A):2$$= ({180^o} - {110^o}):2 = {35^o}$

HĐ 3

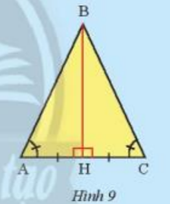
Cho tam giác ABC có $\widehat A$=$\widehat C$. Vẽ đường thẳng đi qua điểm B, vuông góc với AC và cắt AC tại điểm H (Hình 9). Em hãy làm theo gợi ý sau để chứng minh BA = BC.

Xét $\Delta AHB$và $\Delta CHB$cùng vuông tại H, ta có:

BH là cạnh góc vuông ?

$\widehat {HAB}$ = $\widehat {HCB}$ suy ra $\widehat {ABH} = \widehat {CBH}$ (?)

Vậy $\Delta AHB = \Delta CHB$. Suy ra BA = BC

Ta chứng minh $\Delta AHB = \Delta CHB$ rồi từ đó suy ra BA = BC

Xét $\Delta AHB$ và $\Delta CHB$ cùng vuông tại H, ta có:

BH là cạnh góc vuông của và

$\widehat {ABH} = \widehat {CBH}$( Do cùng bằng ${90^o} - \widehat {HAB} = {90^o} - \widehat {HCB}$ )

$\Rightarrow$ $\Delta AHB = \Delta CHB$

$\Rightarrow$ BA = BC

Thực hành 3

Tìm các tam giác cân trong Hình 11 và đánh dấu vào các cạnh bằng nhau.

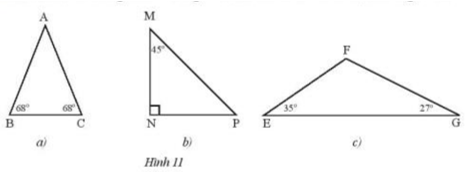
Ta tìm các tam giác cân từ các góc ở đáy rồi suy ra các cạnh bằng nhau

a) Ta có tam giác ABC cân tại A do 2 góc đáy B, C cùng bằng 68°

Nên AB = AC

b) Vì tổng các góc trong tam giác = 180° nên $\widehat M + \widehat N + \widehat P = {180^o}$

$\Rightarrow \widehat P = {180^o} - {45^o} - {90^o} = {45^o}$

$\Rightarrow$ $\Delta MNP$ vuông cân tại N

$\Rightarrow$ MN = NP

c) Xét $\Delta EFG$ theo định lí về tổng số đo các góc trong tam giác ta có :

$\Rightarrow \widehat F + \widehat E + \widehat G = {180^o}$

$\Rightarrow \widehat F = {180^o} - {35^o} - {27^o} = {118^o}$

$\Rightarrow \Delta EFG$ không cân nên không có các cặp cạnh bằng nhau

Vận dụng 2

Cho tam giác ABC cân tại A có góc B bằng ${60^o}$. Chứng minh rằng tam giác ABC đều.

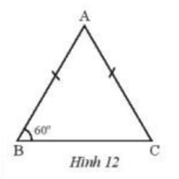
Ta chứng minh 3 góc của tam giác đều bằng ${60^o}$

Ta có: tam giác ABC cân tại A

Nên $\widehat B = \widehat C = {60^o}$( 2 góc đáy của tam giác cân )

Theo định lí về tổng 3 góc trong tam giác ta có : $\widehat A + \widehat B + \widehat C = {180^o}$

$\Rightarrow \widehat A = {180^o} - {60^o} - {60^o} = {60^o}$

Vì $\widehat A = \widehat B = \widehat C = {60^o}$$\Rightarrow$ tam giác ABC là tam giác đều