Giải bài 9.20 trang 76 SGK Toán lớp 7 tập 2 Kết nối tri thức với cuộc sống - Bài 34: Sự đồng quy của ba đường trung tuyến - ba đường phân giác trong một tam giác
![]()
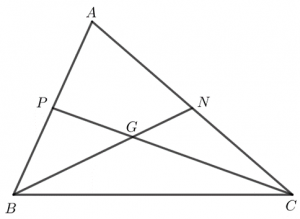
Cho tam giác ABC với hai đường trung tuyến BN, CP và trọng tâm G. Hãy tìm số thích hợp đặt vào dấu “?” để được các đẳng thức:
BG = ? BN, CG = ? CP;
BG = ? GN, CG = ? GP.
![]()
Advertisements (Quảng cáo)
Vì G là trọng tâm của \(\Delta ABC\) nên \(BG = \dfrac{2}{3}BN,CG = \dfrac{2}{3}CP\)
Ta có: GN = BN – BG = BN - \(\dfrac{2}{3}\)BN = \(\dfrac{1}{3}\)BN; GP = CP – CG = CP - \(\dfrac{2}{3}\)CP = \(\dfrac{1}{3}\)CP
Do đó, BN = 3. GN ; CP = 3. GP
Như vậy, \(BG = \dfrac{2}{3}BN = \dfrac{2}{3}.3.GN = 2GN;CG = \dfrac{2}{3}CP = \dfrac{2}{3}.3.GP = 2GP\)
Vậy \(BG = \dfrac{2}{3}BN,CG = \dfrac{2}{3}CP\);
BG = 2GN; CG = 2GP.
