
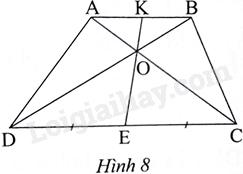
Cho hình thang ABCD (AB//CD) và \(DE = EC\) (Hình 8). Gọi O là giao điểm của AC và BD, K là giao điểm của EO và AB. Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
(I) \(\frac{{AK}}{{EC}} = \frac{{KB}}{{DE}}\), (II) \(AK = KB\), (III) \(\frac{{AO}}{{AC}} = \frac{{AB}}{{DC}}\), (IV) \(\frac{{AK}}{{EC}} = \frac{{OB}}{{OD}}\)
A. 1.
B. 2.
C. 3.
D. 4.

Advertisements (Quảng cáo)
Sử dụng kiến thức về hệ quả định lí Thalès trong tam giác để tìm câu đúng: Nếu một đường thẳng cắt hai cạnh của một tam giác song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

Tam giác AKO có AK//CE nên theo hệ quả định lí Thalès ta có: \(\frac{{AK}}{{CE}} = \frac{{KO}}{{EO}} = \frac{{AO}}{{OC}}\)
Tam giác BKO có BK//DE nên theo hệ quả định lí Thalès ta có: \(\frac{{BK}}{{DE}} = \frac{{KO}}{{EO}} = \frac{{OB}}{{OD}}\)
Do đó, \(\frac{{AK}}{{EC}} = \frac{{KB}}{{DE}}\) và \(\frac{{AK}}{{EC}} = \frac{{OB}}{{OD}}\)
Mà \(DE = EC\) nên \(AK = KB\)
Ta có: \(\frac{{AO}}{{OC}} = \frac{{AK}}{{CE}} = \frac{{2AK}}{{2CE}} = \frac{{AB}}{{DC}}\)
Vậy có 3 khẳng định đúng.
Chọn C.
