
Cho $\Delta ABC\backsim \Delta MNP$ theo tỉ số đồng dạng $k=\frac{AB}{MN}=\frac{2}{3}$. Kẻ đường cao AH của tam giác ABC và đường cao MK của tam giác MNP.
a) Chứng minh rằng $\Delta ABH\backsim \Delta MNK$. Tính tỉ số $\frac{AH}{MK}$.
b) Biết diện tích tam giác ABC bằng $56c{{m}^{2}}$. Tính diện tích tam giác MNP.

Sử dụng kiến thức về áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông: Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Advertisements (Quảng cáo)

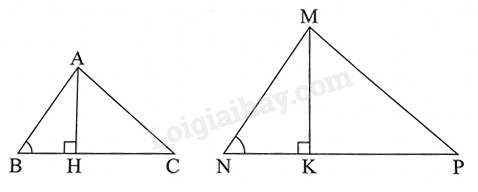
a) Vì $\Delta ABC\backsim \Delta MNP$ (gt) nên $\widehat{B}=\widehat{N}$
Tam giác ABH và tam giác MNK có: $\widehat{AHB}=\widehat{MKN}={{90}^{0}},\widehat{B}=\widehat{N}$
Do đó, $\Delta ABH\backsim \Delta MNK\left( g.g \right)$, do đó $\frac{AH}{MK}=\frac{AB}{MN}=\frac{2}{3}$
b) Vì $\Delta ABC\backsim \Delta MNP$ nên $\frac{{{S}_{\Delta ABC}}}{{{S}_{\Delta MNP}}}={{k}^{2}}$, hay $\frac{56}{{{S}_{\Delta MNP}}}={{\left( \frac{2}{3} \right)}^{2}}$, vậy ${{S}_{\Delta MNP}}=126\left( c{{m}^{2}} \right)$
