
Cho tam giác ABC vuông tại A và đường cao AH.
a) Chứng minh rằng \(A{B^2} = BH.BC\).
b) Chứng minh rằng \(A{H^2} = BH.CH\).
c) Trên tia đối của tia AC lấy điểm D \(\left( {AD < AC} \right)\). Đường thẳng qua H và song song với AC cắt AB, BD lần lượt tại M, N. Chứng minh rằng \(\frac{{MN}}{{MH}} = \frac{{AD}}{{AC}}\).
d) Vẽ AE vuông góc với BD tại E. Chứng minh rằng \(\widehat {BEH} = \widehat {BAH}\).

+ Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g) để tính: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
+ Sử dụng kiến thức về trường hợp đồng dạng thứ hai của hai tam giác (c.g.c) để tính chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng với nhau.

Advertisements (Quảng cáo)
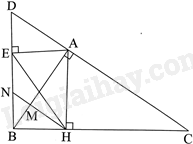
a) Chứng minh được $\Delta ABC\backsim \Delta HBA\left( g.g \right)$ nên \(\frac{{AB}}{{HB}} = \frac{{BC}}{{AB}}\), do đó, \(A{B^2} = BH.BC\)
b) Chứng minh được $\Delta HBA\backsim \Delta HAC\left( g.g \right)$ nên \(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\), do đó \(A{H^2} = BH.CH\).
c) Tam giác ABD có MN//AD nên \(\frac{{MN}}{{AD}} = \frac{{BM}}{{BA}}\left( 1 \right)\)
Tam giác ABC có MH//AC nên \(\frac{{MH}}{{AC}} = \frac{{BM}}{{BA}}\left( 2 \right)\)
Từ (1) và (2) ta có: \(\frac{{MN}}{{AD}} = \frac{{MH}}{{AC}}\) hay \(\frac{{MN}}{{MH}} = \frac{{AD}}{{AC}}\)
d) Chứng minh được $\Delta ABD\backsim \Delta EBA\left( g.g \right)$, suy ra \(\frac{{AB}}{{BE}} = \frac{{BD}}{{AB}}\) hay \(A{B^2} = BE.BD\)
Mà \(A{B^2} = BH.BC\) nên \(BE.BD = BH.BC\), hay \(\frac{{BH}}{{BD}} = \frac{{BE}}{{BC}}\)
Xét tam giác BEH và tam giác BCD ta có: \(\frac{{BH}}{{BD}} = \frac{{BE}}{{BC}}\) góc DBC chung. Do đó, $\Delta BEH\backsim \Delta BCD\left( c.g.c \right)$
Suy ra \(\widehat {BEH} = \widehat {BCD}\). Mà \(\widehat {BAH} = \widehat {BCD}\) (cùng phụ với góc HAC). Vậy \(\widehat {BEH} = \widehat {BAH}\)
