
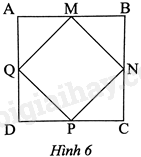
Cho hình vuông ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA (Hình 6). Đẳng thức nào sau đây là đúng?
A. \({S_{MNPQ}} = \frac{1}{4}{S_{ABCD}}\).
B. \({S_{MNPQ}} = \frac{1}{3}{S_{ABCD}}\).
C. \({S_{MNPQ}} = {S_{ABCD}}\).
D. \({S_{MNPQ}} = \frac{1}{2}{S_{ABCD}}\).

+ Sử dụng kiến thức diện tích hình vuông: Diện tích hình vuông có độ dài cạnh bằng a là: \(S = {a^2}\)
+ Sử dụng kiến thức diện tích tam giác vuông: Diện tích tam giác vuông bằng một nửa độ dài hai cạnh hình vuông.

Advertisements (Quảng cáo)
Gọi độ dài cạnh của hình vuông ABCD bằng a.
Vì ABCD là hình vuông nên \(\widehat A = \widehat B = \widehat C = \widehat D = {90^0},AB = BC = CD = DA = a\)
Vì M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên \(AM = MB = BN = NC = PC = PD = QD = QA = \frac{a}{2}\)
Diện tích hình vuông ABCD là: \({S_{ABCD}} = A{B^2} = {a^2}\)
Diện tích tam giác vuông QAM vuông tại A là: \({S_1} = \frac{1}{2}AM.AQ = \frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^2}}}{8}\)
Diện tích tam giác vuông BNM vuông tại B là: \({S_2} = \frac{1}{2}BM.BN = \frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^2}}}{8}\)
Diện tích tam giác vuông PNC vuông tại C là: \({S_3} = \frac{1}{2}CN.PC = \frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^2}}}{8}\)
Diện tích tam giác vuông QDP vuông tại D là: \({S_4} = \frac{1}{2}DP.DQ = \frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^2}}}{8}\)
Do đó, \({S_{MNPQ}} = {S_{ABCD}} - {S_1} - {S_2} - {S_3} - {S_4} = {a^2} - 4.\frac{{{a^2}}}{8} = \frac{{{a^2}}}{2}\)
Suy ra: \({S_{MNPQ}} = \frac{1}{2}{S_{ABCD}}\)
Chọn D.
