
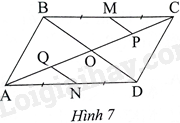
Cho hình bình hành ABCD có M, N lần lượt là trung điểm của BC, AD. Vẽ MP//BD \(\left( {P \in AC} \right)\) và \(NQ//BD\left( {Q \in AC} \right)\). Phát biểu nào sau đây đúng?
A. \(AQ = QP = PC\).
B. O là trung điểm PQ.
C. MNPQ là hình bình hành.
D. MNPQ là hình chữ nhật.

Sử dụng kiến thức về tính chất của đường trung bình của tam giác để chứng minh: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Advertisements (Quảng cáo)

Vì ABCD là hình bình hành nên \(AO = OC,OB = OD\)
Tam giác BOC có: M là trung điểm của BC, MP//BD nên \(CP = OP = \frac{1}{2}OC\)
Tam giác BOC có: M là trung điểm của BC, P là trung điểm của OC nên MP là đường trung bình của tam giác, do đó: \(MP = \frac{1}{2}OB\)
Tam giác AOD có: N là trung điểm của AD, \(NQ//BD\) nên \(AQ = OQ = \frac{1}{2}OA\)
Tam giác AOD có: N là trung điểm của AD, Q là trung điểm của OA nên NQ là đường trung bình của tam giác, do đó: \(QN = \frac{1}{2}OD\)
Vì \(AO = OC\), \(CP = OP = \frac{1}{2}OC\), \(AQ = OQ = \frac{1}{2}OA\) nên \(AQ = OQ = OP = PC\). Do đó, O là trung điểm của PQ.
Vì MP//QN (cùng song song với BD), \(MP = \frac{1}{2}OB = \frac{1}{2}OD = QN\) nên tứ giác MPNQ là hình bình hành.
Chọn B.
